Applications of
Conformal Mappings

Hydrodynamics

If we have a (steady-state) incompressible, nonviscous fluid, we are interested in finding its velocity field $$\mathbf V (x,y)= \left(u(x,y), v(x,y)\right).$$ From vector analysis we know that 'incompressible' means that the divergence $\text{div}\,\mathbf V =0.$ (We say $\mathbf V$ is divergence free.) We assume that $\mathbf V$ is also a potential flow and hence is circulation free; that is $\mathbf V = \text{grad } \phi $ for some $\phi$ called the velocity potential. Thus $\phi$ is harmonic because $$\nabla^2\phi = \text{div } \text{grad }\phi = \text{div } \mathbf V=0.$$ Thus when we solve for $\phi$ we can obtain $\mathbf V$ by taking $\mathbf V = \text{grad } \phi$. That is \begin{eqnarray*} u=\frac{\partial \phi }{\partial x},\quad v=\frac{\partial \phi }{\partial y}. \end{eqnarray*}

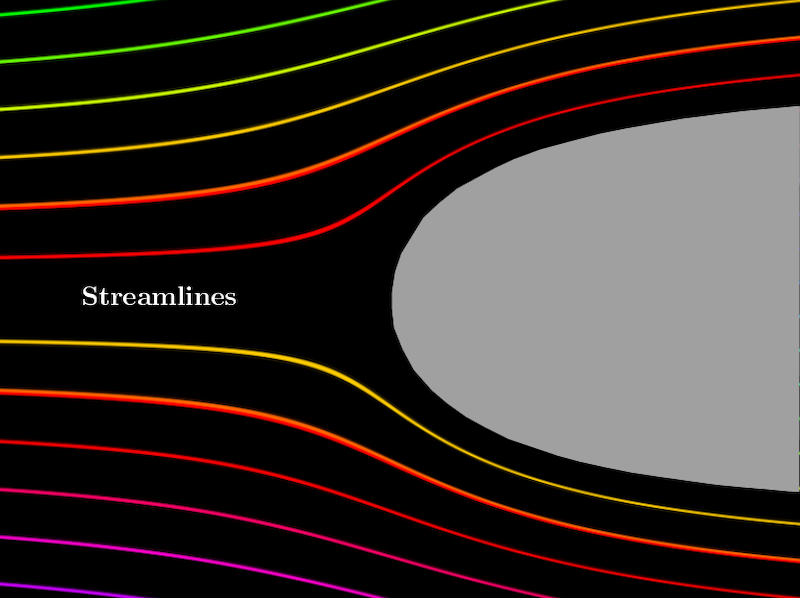
The conjugate $\psi$ of the harmonic function $\phi$ (which will exist on any simple connected region) is called the stream function, and the analytic function $$F=\phi +i\psi$$ is called the complex potential.

The stream function must satisfy \begin{eqnarray*} u=\frac{\partial \psi }{\partial y},\quad v=-\frac{\partial \psi }{\partial x}. \end{eqnarray*} Finally, lines of constant $\psi$ have $\mathbf V$ as their tangents, so lines of constant $\psi$ may be interpreted as the lines along which particles of fluid move; hence the name stream function.