Uniform Flow Around a Circle

Consider a uniform flow at speed $U$ in the $x$-direction, with complex potential $F(z)=Uz.$ If we insert an impermeable circular obstacle, at $|z|=a$ say, then the flow will be disturbed as illustrated in the image below. The challenge here is to calculate the disturbed flow.

Here we can use a well known result in fluid dynamics established by the English mathematician L. M. Milne-Thompson:

Suppose a complex potential $F(z)$ is given such that any singularities in $F(z)$ occur in $|z|\gt a.$ Then the potential \begin{eqnarray}\label{circle-theorem} w = F(z) + \overline{F\left(\frac{a^2}{\overline{z}}\right)} \end{eqnarray} (where the bar denotes complex conjugate) has the same singularities as $F(z)$ in $|z|\gt a$ and the circle $|z|=a$ is a streamline.

Let $F(z)$ be a complex potential such that any singularities occur only in the region $|z|\gt a$ (with $a>0$) and define \begin{eqnarray}\label{circle-01} w = F(z) + \overline{F\left(\frac{a^2}{\overline{z}}\right)}. \end{eqnarray} Notice that if $|z|\gt a,$ then $\big|a^2/\,\overline{z}\big|\lt a.$ Thus, since $F(z)$ has no singularities in $|z|\leq a,$ it follows that the second term in (\ref{circle-01}) has no singularities in $|z|\gt a.$ This means that $F$ and $w$ have the same singularities in $|z|\gt a.$

Now we are interested to know what happens on the circular boundary $|z|=a.$ In this case we have that $\overline{z} \cdot z = a^2.$ That is $$z= \frac{a^2}{\overline{z} }.$$ Thus $$\big. w \big|_{|z|=a}= F(z)+ \overline{F\left(\frac{a^2}{\overline{z}}\right)} = F(z) + \overline{F\left(z\right)} = 2 \text{Re}\left(f(z)\right),$$ which is entirely real. Therefore on the boundary $|z|=a$ $$\psi = \text{Im}\, w = 0.$$ This shows that the circle $|z|=a$ is a streamline.

Notice that the complex potential $F(z)=Uz$ satisfies the hypothesis of the Circle Theorem. We can therefore obtain the complex potential of the uniform flow around a circle by substituting $F(z)=Uz$ into equation (\ref{circle-theorem}): \begin{eqnarray}\label{potential} w = Uz + \overline{\frac{Ua^2}{\overline{z}}} = Uz + \frac{Ua^2}{z}. \end{eqnarray}

Consequently, the streamfunction is just the imaginary part of (\ref{potential}), namely \begin{eqnarray*} \psi = Uy\left(1- \frac{a^2}{x^2+y^2} \right). \end{eqnarray*} and we can see that the circle $x^2+y^2=a^2$ is indeed a streamline, with $\psi=0.$ The resulting flow is shown in Figure 2 with $a=1.$

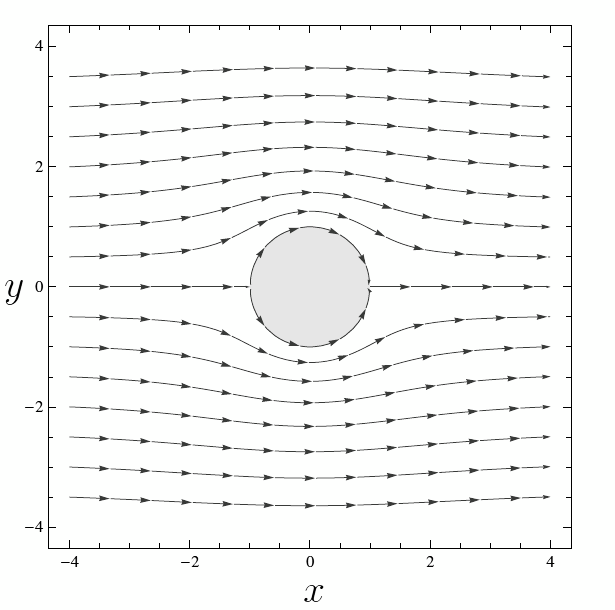
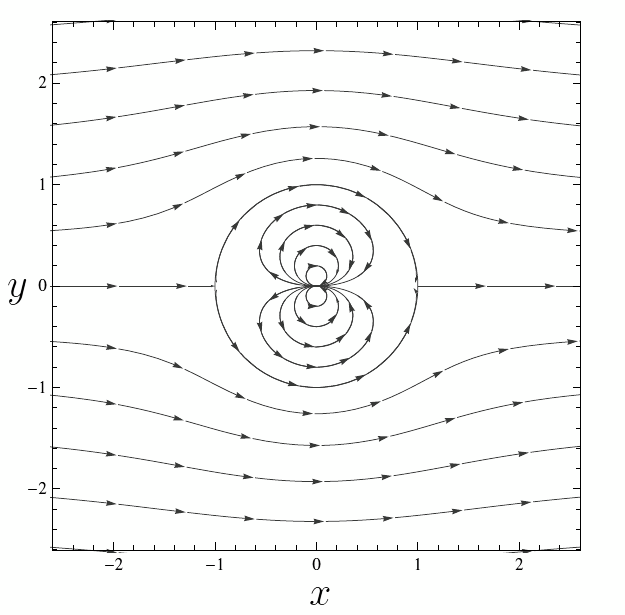
You probably have noticed that (\ref{potential}) has a singularity at $z=0.$ This kind of singularity is known as a doublet and corresponds to the function $Ua^2/z.$ The singularity at the origin is inside the obstacle and thus does not affect the external flow. The full streamline pattern, including the doublet inside the circle, is shown in Figure 3.

Exercise: Show that the components of velocity field $\mathbf V = (u, v)$ for the uniform flow around a circle are given by

\begin{eqnarray*} u = U\left(1 - a^2\frac{x^2-y^2}{\left(x^2+y^2\right)^2}\right),\quad v= -2 U^{2} a^{2} \frac{ x y}{ \left(x^{2} + y^{2} \right)^{2}} \end{eqnarray*}

where $U$ is the speed and $a$ is the radius.

Uniform flow around circle with circulation

If we add a vortex to the complex potential defined in (\ref{potential}), we obtain a uniform flow around a circle with circulation: \begin{eqnarray}\label{circulation} w = Uz + \frac{Ua^2}{z} - \frac{iC}{2\pi}\log z, \end{eqnarray} where $C\in \mathbb R$ represents the circulation about the circle.

In this case, the streamfunction is

\begin{eqnarray*} \psi = U y \left( 1 - \frac{a^2}{x^2+y^2} \right) - \frac{C}{4\pi} \log\left(x^2+y^2\right). \end{eqnarray*}

Notice that the circle $x^2+y^2=a^2$ is still a streamline, with $\psi = - (C/2\pi)\log a.$ Any stagnation point in the flow satisfies the equation $$0 = U - \frac{Ua^2}{z^2} - \frac{iC}{2\pi z},$$ which can be rearranged to the quadratic equation $$z^2-2i\gamma a z - a^2 = 0, \quad \text{with}\quad \gamma =\frac{C}{4\pi Ua}.$$ The roots of this equation are $$\frac{z}{a} = i\gamma \pm \sqrt{1-\gamma^2}.$$

Thus when $\gamma = 0,$ there is no circulation with stagnation points at $z =\pm a.$ As $\gamma$ increases, the anticlockwise circulation causes the stagnation points to move upwards around the circle. When it reaches the value 1, the two stagnation points coalesce at the top of the cylinder $z = ia.$ If $\gamma > 1,$ then one stagnation point moves into the flow; the other one is inside the circle.

Explore all the cases in the applet below which shows the flow and a circle of radius 1. Drag the sliders $U$ and $C$ to change speed and circulation, respectively.

Exercise: Show that the components of velocity field $\mathbf V = (u, v)$ for the uniform flow around a circle with circulation are given by

\begin{eqnarray*} u &=& U\left(1 - a^2\frac{x^2-y^2}{\left(x^2+y^2\right)^2}\right) - \frac{C}{2\pi}\frac{y}{x^2+y^2},\\ v &=& -2 U^{2} a^{2} \frac{ x y}{ \left(x^{2} + y^{2} \right)^{2}} + \frac{C}{2\pi}\frac{x}{x^2+y^2} \end{eqnarray*}

where $U$ is the speed, $a$ is the radius and $C$ is the circulation.