←Complex Analysis→

Topology of the Complex Plane

Neighbourhoods

An $\varepsilon$ neighbourhood, also called open ball or open disk, of a complex number $z_0$ consists of all points $z$ lying inside but not on a circle centred at $z_0$ and with radius $\varepsilon>0$ and is expressed by \begin{eqnarray} B_{\varepsilon}(z_0)=\{z:|z-z_0| \lt \varepsilon\} \end{eqnarray} The closed $\varepsilon$ neighbourhood of $z_0$ is expressed by \begin{eqnarray} \overline{B}_{\varepsilon}(z_0)=\{z:|z-z_0|\leq \varepsilon\} \end{eqnarray} And finally, a deleted $\varepsilon$ neighbourhood of $z_0$, also called punctured balls or disks, is expressed by \begin{eqnarray} B_{\varepsilon}(z_0)\setminus \{z_0\}=\{z:0 \lt |z-z_0| \lt \varepsilon\} \end{eqnarray} Figure 1 shows the geometrical representation of the following examples:

  1. $B_{1}(0)=\{z:|z|\lt 1\}$
  2. $\overline{B}_{\frac{7}{8}}\left(-1-\sqrt{2}i\right)=\left\{z:|z-\left(-1-\sqrt{2}i\right)|\leq \frac{7}{8}\right\}$
  3. $\overline{B}_{\frac{1}{2}}\left(2+\sqrt{3}i\right)\setminus \left\{2+\sqrt{3}i\right\}=\left\{z:0 \lt |z-\left(2+\sqrt{3}i\right)|\leq\frac{1}{2}\right\}$
Neighbourhoods
Figure 1: Geometrical representation of neighbourhoods.

Classification of points

A point $z_0$ is said to be an interior point of a set $S\subset \mathbb C$ whenever there is some neighbourhood of $z_0$ that contains only points of $S$; it is called an exterior point of $S$ when there exists a neighbourhood of it containing no points of $S$. If $z_0$ is neither of these, it is a boundary point of $S$. A boundary point is, therefore, a point all of whose neighbourhoods contain at least one point in $S$ and at least one point not in $S$. The totality of all boundary points is called the boundary of $S$.

In this text we will use the following notation:

  1. $\text{Int } S=\left\{z: z \text{ is an interior point of } S \right\}$
  2. $\text{Ext } S=\left\{z: z \text{ is an exterior point of } S \right\}$
  3. $\partial S=\left\{z: z \text{ is a boundary point of } S \right\}$

Interior, boundary, and exterior S
Figure 2: Interior, boundary, and exterior of set $S$.

Considering the previous examples of neighbourhoods, let $$ S_1=B_1(0),\; S_2=\overline{B}_{\frac{7}{8}}\left(-1-\sqrt{2}i\right) \text{ and } S_3=\overline{B}_{\frac{1}{2}}\left(2+\sqrt{3}i\right)\setminus \left\{2+\sqrt{3}i\right\}. $$ Thus, for $S_1$ we have:

For $S_2$ we have:

And finally, for $S_3$ we have:

Topological space

A set $S$ is open if for every $z\in S$, exits $\varepsilon>0$ such that $$B_{\varepsilon}(z)\subset S.$$ That is, $\text{Int } S= S$. A set $S$ is closed if it contains all of its boundary points, that is $$\partial S\subseteq S.$$ The set $\mathbb C$ is both open and closed since it has no boundary points.

The set $\mathbb C$, together with the collection $\tau =\{S\subseteq \mathbb C: S \text{ is open} \}$ is a topological space, and this is expressed by the pair $\left(\mathbb C, \tau\right)$. The topological space $\left(\mathbb C, \tau\right)$ satisfies the following:

  1. $\emptyset$ and $\mathbb C$ are open.
  2. Whenever two or more sets are open, then so is their union.
  3. Whenever sets $S_1$ and $S_2$ are open, then so is $S_1\bigcap S_2$.

Remark: The technical definition of topological space is a bit unintuitive, particularly if you haven't studied topology. In essence, it states that the geometric properties of subsets of $\mathbb C$ will be preserved when continuous transformations (functions or mappings) are applied.

The closure of a set $S$ is the closed set consisting of all points in $S$ together with the boundary of $S$. In other words $$\overline{S}=S\cup \partial S.$$

An open set $S$ is connected if each pair of points $z_1$ and $z_2$ in it can be joined by a polygonal line, consisting of a finite number of line segments joined end to end, that lies entirely in $S$.

Connected set
Figure 3: Connected set.

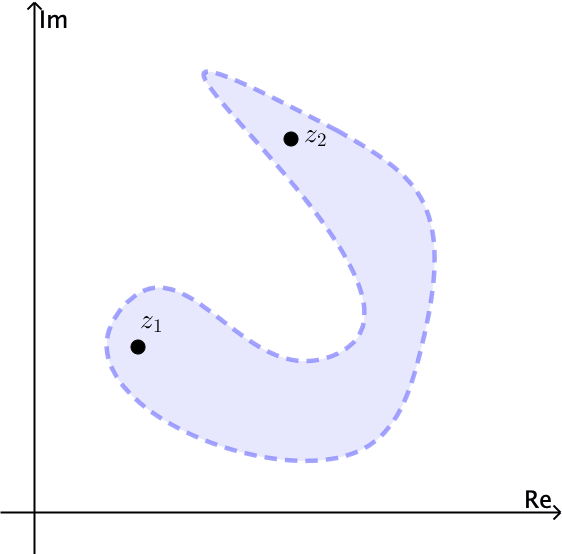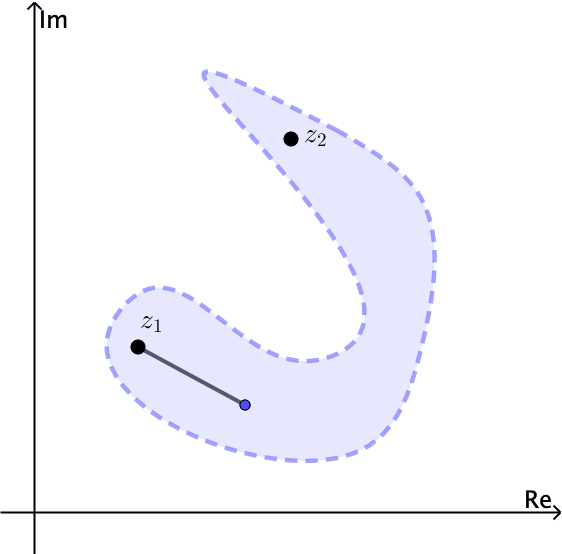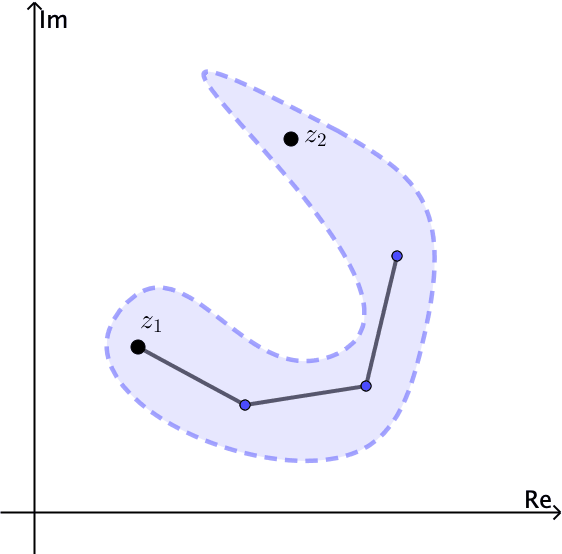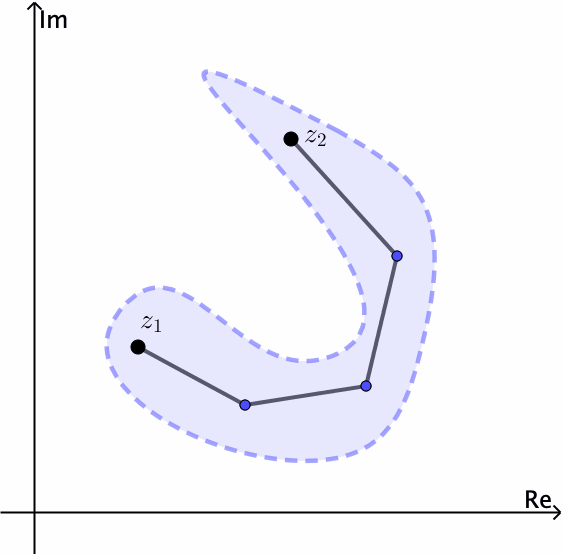
Notice for example that the open set $|z| \lt 1$ is connected. The annulus $1 \lt |z| \lt 2$ is open and also connected, see Figures 4 and 5.

Open connected set
Figure 4: $|z| \lt 1$.
Annulus
Figure 5: $1 \lt |z| \lt 2$.

A nonempty open set that is connected is called a domain. In this context, any neighbourhood is a domain. A domain together with some, none, or all of its boundary points is referred to as a region. In other words, a set whose interior is a domain is called a region. A set $S$ is bounded if there is $R>0$ such that $$S\subset B_R(0)=\{z\in \mathbb C: |z|\lt R\}.$$

Bounded set
Figure 6: Bounded set.

Exercise: Sketch the set $S$ of points in the complex plane satisfying the given inequality. Determine whether the set is (a) open, (b) closed, (c) a domain, (d) bounded, or (e) connected.


NEXT: Complex Functions