Complex Integration

Contour integral

Consider a contour $C$ parametrized by $z(t) = x(t) + i y(t)$ for $a\leq t\leq b.$ We define the integral of the complex function along $C$ to be the complex number \begin{eqnarray}\label{contour-integral} \int_C f(z)\,dz = \int_a^bf\left(z(t)\right)z'(t)\,dt. \end{eqnarray} Here we assume that $f\left(z(t)\right)$ is piecewise continuous on the interval $a \leq t \leq b$ and refer to the function $f (z)$ as being piecewise continuous on $C.$ Since $C$ is a contour, $z'(t)$ is also piecewise continuous on $a \leq t \leq b$; and so the existence of integral (\ref{contour-integral}) is ensured.

The right hand side of (\ref{contour-integral}) is an ordinary real integral of a complex-valued function; that is, if $w(t) = u(t) + i v(t),$ then \begin{eqnarray}\label{integral-real-cv} \int_a^b w(t)\,dt = \int_a^b u(t)\,dt + i \int_a^b v(t)\,dt \end{eqnarray}

Now let us write the integrand $$f(z)= u(x,y)+ iv(x,y)$$ in terms of its real and imaginary parts, as well as the differential $$dz=\frac{dz}{dt}dt = \left(\frac{dx}{dt}+ i \frac{dy}{dt}\right)dt = dx+ i dy$$ Then the complex integral (\ref{contour-integral}) splits up into a pair of real line integrals:

Example 1: Let's evaluate $\int_C \overline{z}\, dz,$ where $C$ is given by $x=3t, y=t^2,$ with $-1\leq t\leq 4.$

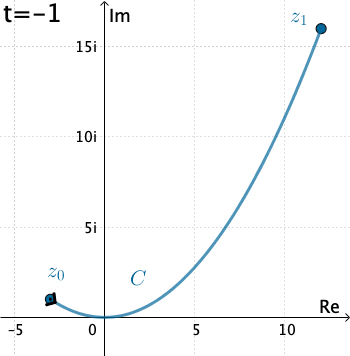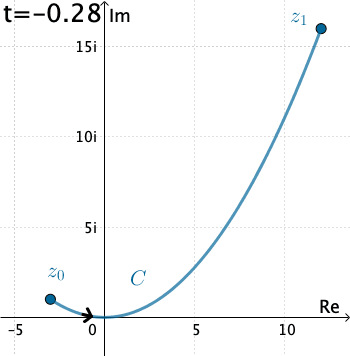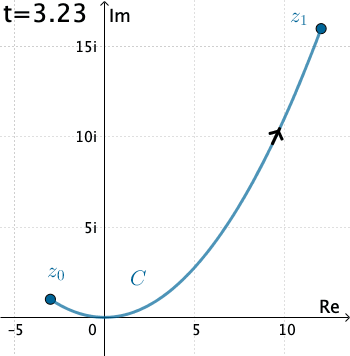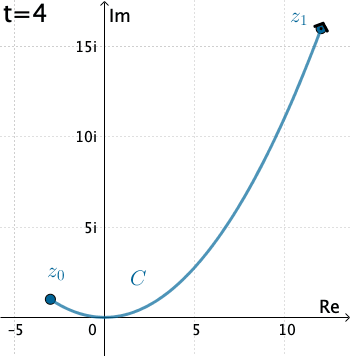
Here we have that $C$ is $z(t)=3t+ it^2 .$ Therefore, with the identification $f(z)=\overline{z}$ we have $$f\left(z(t)\right)=\overline{3t+it^2}= 3t-it^2 .$$ Also, $z'(t) = 3 + 2it,$ and so the integral is \begin{eqnarray*} \int_C \overline{z}\, dz&=& \int_{-1}^4 \left(3t-it^2\right)\left(3+ 2it\right)dt\\ &=& \int_{-1}^4 \left(2t^3+9t + 3t^2i\right)dt\\ &=& \int_{-1}^4 \left(2t^3+9t \right)dt + i\int_{-1}^4 3t^2dt\\ &=& \Bigg. \left(\frac{1}{2}t^4 + \frac{9}{2} t^2\right)\Bigg|_{-1}^4 + i\Bigg. t^3\Bigg|_{-1}^4\\ &=& 195+ 65 i. \end{eqnarray*}

Example 2: Now let's evaluate $\displaystyle \int_C \dfrac{1}{z}\, dz,$ where $C$ is the circle $x=\cos t, y=\sin t,$ with $0\leq t\leq 2\pi .$

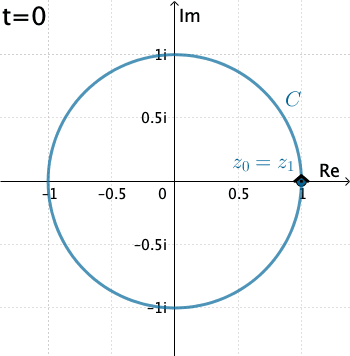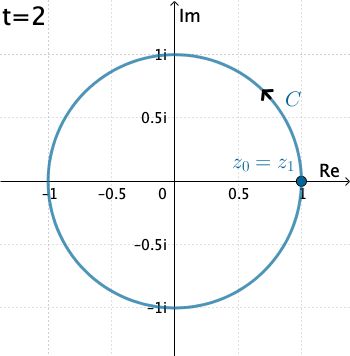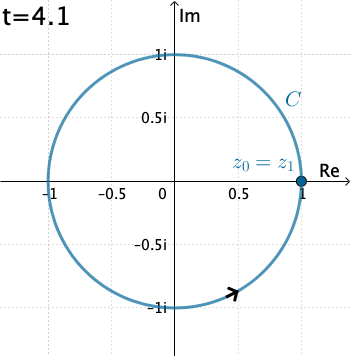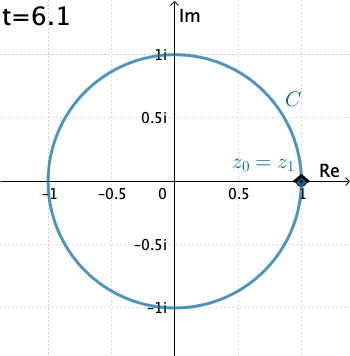
In this case $C$ is $z(t)=\cos t + i \sin t = e^{it},$ $$f\left(z(t)\right)=\frac{1}{e^{it}}$$ and, $z'(t) = ie^{it}.$ Thus \begin{eqnarray*} \int_C \dfrac{1}{z}\, dz&=& \int_{0}^{2\pi} \left(e^{-it}\right)ie^{it}dt = i \int_{0}^{2\pi} dt= 2\pi \,i. \end{eqnarray*}

Numerical evaluation of complex integrals

Exploration 1

Use the following applet to explore numerically the integral $$\int_C \overline{z}\, dz$$ with different contours $C$:

• Line segments.
• Semicircles.
• Circles, positively and negatively oriented.

You can also change the domain coloring plotting option. Drag the points around and observe carefully what happens. Then solve Exercise 1 below.

The arrows on the contours indicate direction.

Exploration 2

Now use the applet below to explore numerically the integrals $$\int_C \left(z^2+z\right) dz;\qquad \int_C \frac{1}{z^2}\, dz$$ with different contours $C$ (line segments, semicircles, and circles). Drag the points around and observe carefully what happens. You can select the functions z^2+z or 1/z^2 from the list at the left-top corner. Then solve Exercises 2 and 3.

Properties

All the following familiar properties of integrals can be proved directly from the definition given in (\ref{integral-real-cv}). If $w(t)= u(t)+iv(t)$ and $s(t)= \upsilon(t)+i \nu(t)$ are complex-valued functions of a real variable $t$ continuous on an interval $[a,b],$ then

From definition (\ref{contour-integral}), and the properties just mentioned above, it also follows immediately that

Now consider the contour defined for the integral (\ref{contour-integral}). The contour $-C$ consists of the same set of points but with the order reversed so that the new contour extends from $z_2$ to $z_1,$ as shown in Figure 3.

The contour $-C$ has a parametric representation $z=z(-t)$ with $-b\leq t \leq -a.$ Hence

If we use the substitution $\tau = -t$ in the last integral, then

Hence, we obtain the following property

Consider now a path $C,$ parametrized by $z(t)$ for $t\in[a,b],$ that consists of a contour $C_1$ from $z_1$ to $z_2$ followed by a contour $C_2$ from $z_2$ to $z_3,$ the initial point of $C_2$ being the final point of $C_1.$ Then

Finally we introduce an inequality involving contour integrals that is extremely important in various applications. Consider $C$ a smooth curve parametrized by $z(t)=x(t)+ iy(t)$ with $t\in [a,b].$ Suppose that the components $x'(t)$ and $y'(t)$ of the derivative \[ z'(t) = x'(t) + iy'(t) \] are continuous on the entire interval $[a,b].$ Then the real-valued function \[ \left|z'(t)\right| =\sqrt{\left[x'(t)\right]^2+ \left[y'(t)\right]^2} \] is integrable on $[a,b].$ According to the definition of arc length from calculus, the length of $C$ is the number \[ L = \int_a^b \left|z'(z)\right|\,dt. \]

If $C$ is a contour of length $L$ and $f$ is a piecewise continuous function on $C,$ and $M$ is a nonnegative constant such that $\left|f(z)\right|\leq M$ for all points $z$ on $C$ at which $f(z)$ is defined, then \begin{eqnarray}\label{ML-inequality} \left|\int_C f(z)\, dz\right|\leq ML \end{eqnarray}

Note that since $C$ is a contour and $f$ is piecewise continuous on $C,$ a number $M$ appearing in the inequality $\left|f(z)\right|\leq M$ will always exist. The reason is that the real-valued function $\left|f\big(z(t )\big)\right|$ is continuous on the closed bounded interval $[a,b]$ when $f$ is continuous on $C;$ and this function always reaches a maximum value $M$ on that interval. Therefore $|f (z)|$ has a maximum value on $C$ when $f$ is continuous on it. This is also true when $f$ is piecewise continuous on $C.$

The property (\ref{ML-inequality}) is often used in the theory of complex integration and is sometimes referred to as the ML-inequality.

Example 3: Let $C$ be the contour of the circle $|z|=2$ from $z_1=2$ to $z_2=2i$ that lies in the first quadrant, as shown in Figure 5. We can use inequality (\ref{ML-inequality}) to show that \[ \left|\int_C \frac{dz}{z^2-1}\right|\leq \frac{\pi}{3}. \] without evaluating the integral.

Note that if $z$ is a point of $C,$ then

\begin{eqnarray*} \left|z^2-1\right|\geq \left|\left|z^2\right|- 1\right|= \left|\left|z\right|^2- 1\right| = \left|4- 1\right|=3 \end{eqnarray*}

Thus \[ \left|\frac{1}{z^2-1}\right| = \frac{1}{ \left|z^2- 1\right|}\leq \frac{1}{3} \] Also the length of $C$ is $\dfrac{1}{4}(4\pi).$ Thus, if we take $M=\dfrac{1}{3}$ and $L= \pi,$ we find that \[ \left|\int_C \frac{dz}{z^2-1}\right|\leq ML = \frac{\pi}{3}. \]

Example 4: We can also use the ML-inequality to find the value of the integral \[ \lim_{R\to \infty} \int_{C_R}\frac{z^{1/2}}{z^2+1}dz \] where $C_R$ is the arc $z(t)= Re^{it},$ with $t\in[0,\pi]$ and $z^{1/2}$ denotes the branch \[ z^{1/2} = \exp\left(\frac{1}{2}\log z\right) = \sqrt{r}e^{it/2},\quad \left(r>0,-\frac{\pi}{2}\lt t \lt \frac{3\pi}{2}\right) \] of the square root function.

Note that when $|z|=R\gt 1,$ then $\abs{z^{1/2}}= \abs{\sqrt{R}e^{it/2}} = \sqrt{R}$ and \[ \abs{z^2+1}\geq \abs{\abs{z^2}-1} = R^2-1. \] Thus, at points on $C_R$, we have

\[ \abs{\frac{z^{1/2}}{z^2+1}}\leq M_R \quad \text{where} \quad M_R = \frac{\sqrt{R}}{R^2-1}. \]

Since the length of $C_R$ is $L=\pi R,$ using (\ref{ML-inequality}), we obtain

\[ \abs{\int_{C_R}\frac{z^{1/2}}{z^2+1}dz}\leq M_R L = \frac{\pi R\sqrt{R}}{R^2-1} \cdot \frac{1/R^2}{1/R^2}= \frac{\dfrac{\pi}{\sqrt{R}}}{1 - \dfrac{1}{R^2}}. \]

The term on the right tends to zero as $R$ tends to infinity. Hence \[ \lim_{R\to \infty} \int_{C_R}\frac{z^{1/2}}{z^2+1}dz=0. \]

Antiderivatives

While the value of a contour integral of a function $f (z)$ from a fixed point $z_0$ to a fixed point $z_1$ generally depends on the chosen path, there are certain functions for which the integrals from $z_0$ to $z_1$ have values that are independent of path, as you have seen in Exercises 2 and 3. These examples also illustrate the fact that the values of integrals around closed paths are sometimes, but not always, zero. The next theorem is useful in determining when integration is independent of path and, moreover, when an integral around a closed path has value zero. This theorem is known as the complex version of the Fundamental Theorem of Calculus and involves the concept of antiderivative (or primitive) of a continuous function $f(z)$ on a domain $D,$ that is, a function $F(z)$ such that $F'(z)=f(z)$ for all $z\in D.$

As a consequence of the previous Theorem 1, for closed curves we have \begin{eqnarray} \int_{C} f\left(z\right)dz=\int_{C}F^{\prime}(z) dz=0. \end{eqnarray} for every closed contour $C,$ that is, the endpoints are equal.

If the function $f(z)$ satisfies the hypothesis of Theorem 1, then for all contours $C$ lying in $D$ beginning at $z_1$ and ending at $z_2$ we have expression (\ref{FTC}). Hence the result demonstrates that the integral is independent of path. This fact is illustrated in Figure 6.

Considering Figure 6, we have $$\int_{C_1} f\left(z\right)dz=\int_{C_2} f\left(z\right)dz$$ because

In addition, we have the following sufficient condition for the existence of an antiderivate:

Consider the function \begin{eqnarray}\label{anti-exists} F(z) = \int_{z_0}^{z}f(s)\,ds \end{eqnarray} where $s$ denotes a complex variable, $z_0$ is a fixed points in $D,$ and $z$ represents any point in $D.$ Assuming that $f$ is continuous and $\ds\int_C f(z)\,dz$ is independent of path, we wish to prove that $F'(z) = f(z),$ that is, (\ref{anti-exists}) is an antiderivate of $f$ in $D.$

Using properties of the integral we have

\begin{eqnarray}\label{anti-def} F(z+ \Delta z) - F(z) = \int_{z_0}^{z+\Delta z}f(s)\,ds - \int_{z_0}^{z}f(s)\,ds = \int_{z}^{z+\Delta z}f(s)\,ds. \end{eqnarray}

Since $D$ is a domain, we can choose $\Delta z$ so that $z + \Delta z$ is in $D.$ Furthermore, $z$ and $z + \Delta z$ can be joined by a straight segment, as shown un Figure 7. This is the contour we use in the last integral in (\ref{anti-def}). For $z$ fixed, we can write

\begin{eqnarray}\label{anti-expand} f(z) \Delta z =f(z) \int_{z}^{z+\Delta z}ds = \int_{z}^{z+\Delta z}f(z)\,ds \quad \text{or}\quad f(z) = \frac{1}{\Delta z} \int_{z}^{z+\Delta z}f(z)\,ds. \end{eqnarray}

From (\ref{anti-def}) and (\ref{anti-expand}) we obtain

\begin{eqnarray*} \frac{F(z+\Delta z)-f(z)}{\Delta z} = \frac{1}{\Delta z} \int_{z}^{z+\Delta z}\left[f(s) - f(z)\right]\,ds. \end{eqnarray*}

Now, since $f$ is continuous, for any $\epsilon\gt 0 $ there exists a $\delta\gt 0$ such that $\abs{f(s)-f(z)}\lt \epsilon$ whenever $\abs{s-z}\lt \delta.$ Thus, if we choose $z+ \Delta z$ close enough to $z$ so that $\abs{\Delta z}\lt \delta,$ it follows from the ML-inequality that

\begin{eqnarray*} \abs{\frac{F(z+\Delta z)-f(z)}{\Delta z} } &= &\abs{\frac{1}{\Delta z} \int_{z}^{z+\Delta z}\left[f(s) - f(z)\right]\,ds}\\ &=& \abs{\frac{1}{\Delta z}} \abs{ \int_{z}^{z+\Delta z}\left[f(s) - f(z)\right]\,ds}\\ &\leq & \abs{\frac{1}{\Delta z}}\epsilon \abs{\Delta z} = \epsilon. \end{eqnarray*}

Therefore, we have proved that

\begin{eqnarray*} \lim_{\Delta z \to 0}\frac{F(z+\Delta z)-f(z)}{\Delta z} = f(z)\quad \text{or}\quad F'(z) = f(z). \end{eqnarray*}