←Complex Analysis→

Curves in the Complex Plane

Suppose the continuous real-valued functions $x = x(t),$ $y = y(t),$ $a \leq t \leq b,$ are parametric equations of a curve $C$ in the complex plane. If we use these equations as the real and imaginary parts in $z = x+iy$, we can describe the points $z$ on $C$ by means of a complex-valued function of a real variable $t$ called a parametrization of $C$: \begin{equation}\label{parcurve} z(t) = x(t) + i y(t), \quad a\leq t\leq b. \end{equation}

The point $z(a) = x(a) + i y(a)$ or $z_0 = (x(a), y(a))$ is called the initial point of $C$ and $z(b) = x(b) + iy(b)$ or $z_1 = (x(b), y(b))$ is its terminal point. The expression $z(t) = x(t) + iy(t)$ could also be interpreted as a two-dimensional vector function. Consequently, $z(a)$ and $z(b)$ can be interpreted as position vectors. As $t$ varies from $t = a$ to $t = b$ we can envision the curve $C$ being traced out by the moving arrowhead of $z(t)$. This can be appreciated in the following applet with $0 \leq t\leq 1$.

Press Start to animate. You can move the points to change the curve.

For example, the parametric equations $x = \cos t,$ $y = \sin t,$ $0 \leq t \leq 2\pi,$ describe a unit circle centered at the origin. A parametrization of this circle is $z(t) = \cos t + i \sin t,$ or $z(t) = e^{it},$ $0 \leq t \leq 2\pi$.

Press Start to animate.

Contours

The notions of curves in the complex plane that are smooth, piecewise smooth, simple, closed, and simple closed are easily formulated in terms of the vector function (\ref{parcurve}). Suppose the derivative of (\ref{parcurve}) is $z'(t) = x'(t) + iy'(t).$ We say a curve $C$ in the complex plane is smooth if $z'(t)$ is continuous and never zero in the interval $a \leq t \leq b.$ As shown in Figure 2, since the vector $z'(t)$ is not zero at any point $P$ on $C$, the vector $z'(t)$ is tangent to $C$ at $P$. Thus, a smooth curve has a continuously turning tangent; or in other words, a smooth curve can have no sharp corners or cusps. See Figure 2.

Smooth curve and Tangent vector
Figure 1: $z'(t)=x'(t) + iy(t)$ as a tangent vector.
Non smooth
Figure 2: Curve $C$ is not smooth since it has a cusp.

A piecewise smooth curve $C$ has a continuously turning tangent, except possibly at the points where the component smooth curves $C_1, C_2, \ldots, C_n$ are joined together.

Piecewise smooth curve
Figure 3: A piecewise smooth curve.

A curve $C$ in the complex plane is said to be a simple if $z(t_1) \neq z(t_2)$ for $t_1 \neq t_2,$ except possibly for $t = a$ and $t = b.$ $C$ is a closed curve if $z(a) = z(b).$

Simple curve
Figure 4: Simple curve.
Non simple curve
Figure 5: Non simple curve.

$C$ is a simple closed curve if $z(t_1)\neq z(t_2)$ for $t_1\neq t_2$ and $z(a) = z(b).$

Simple curve
Figure 4: Simple closed curve.
Non simple curve
Figure 5: Non simple closed curve.

In complex analysis, a piecewise smooth curve $C$ is called a contour or path. We define the positive direction on a contour $C$ to be the direction on the curve corresponding to increasing values of the parameter $t$. It is also said that the curve $C$ has positive orientation. In the case of a simple closed contour $C$, the positive direction corresponds to the counterclockwise direction. For example, the circle $z(t) = e^{it}$, $0 \leq t \leq 2\pi$, has positive orientation. The negative direction on a contour $C$ is the direction opposite the positive direction. If $C$ has an orientation, the opposite curve, that is, a curve with opposite orientation, is denoted by $−C$. On a simple closed curve, the negative direction corresponds to the clockwise direction. For instance, the circle $z(t) = e^{-it}$, $0 \leq t \leq 2\pi$, has negative orientation.

Simple curve
Figure 6: Positively oriented.
Non simple curve
Figure 7: Negatively oriented.

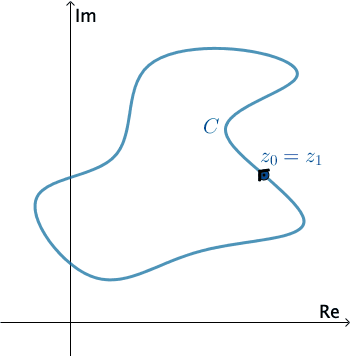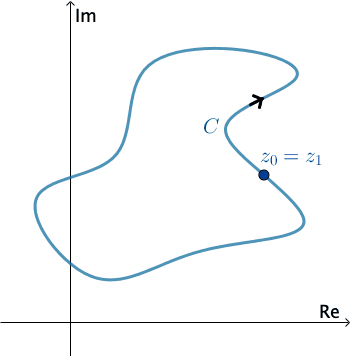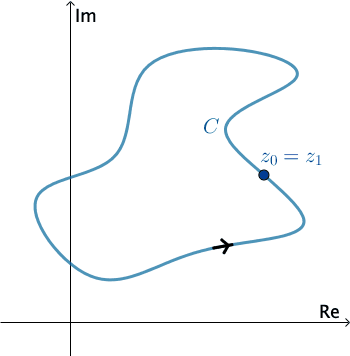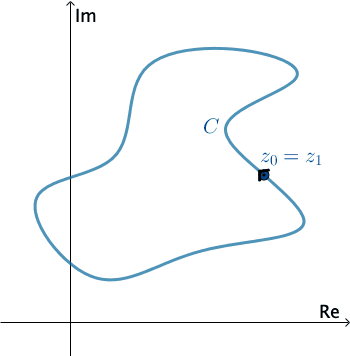
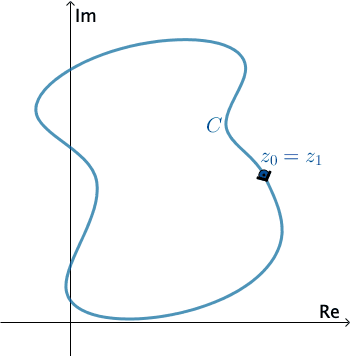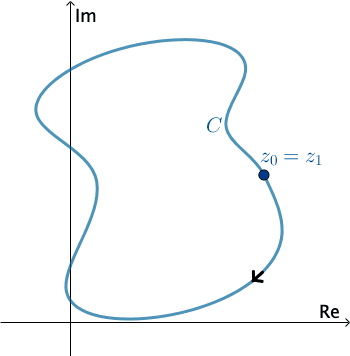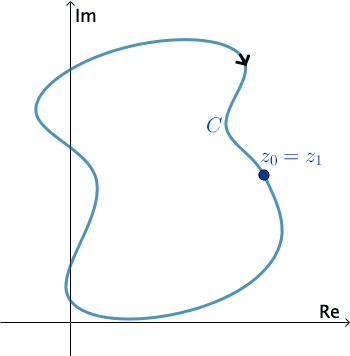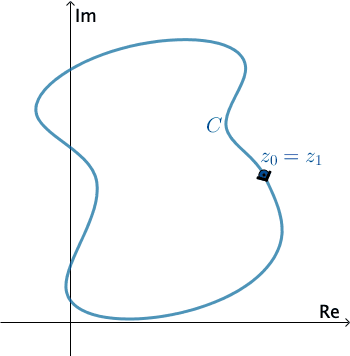
Press Start to animate. You can change the direction of $C$.

Exercise: There is no unique parametrization for a contour $C$. You should verify that \begin{eqnarray*} z(t)&=&e^{it} =\cos t+i\sin t,\; 0\leq t\leq 2\pi \\ z(t)&=& e^{2\pi it} =\cos \left(2 \pi t\right) +i \sin \left(2 \pi t\right),\; 0\leq t\leq 1\\ z(t)&=&e^{\pi/2 it} =\cos \left( \frac{\pi}{2} t\right)+i \sin \left( \frac{\pi}{2} t\right),\; 0\leq t \leq 4 \end{eqnarray*} are all parametrizations, oriented in the positive direction, for the unit circle $|z| = 1$.


NEXT: Complex Integration