Loading...
Cauchy Integral Formula Table of Contents Complex Analysis Series


The Fundamental Theorem
of Algebra

Consider the polynomial

\begin{eqnarray}\label{example-001} p(z) = z^8-2z^7+2z^6-4z^5+2z^4-2z^3-5z^2+4z-4 \end{eqnarray}

The Fundamental Theorem of Algebra states that: Every nonconstant polynomial with complex coefficients has a root in the complex numbers.

Polynomial of degree 8
Enhaced phase portrait of $p(z),$ with level curves of $\abs{p(z)}.$

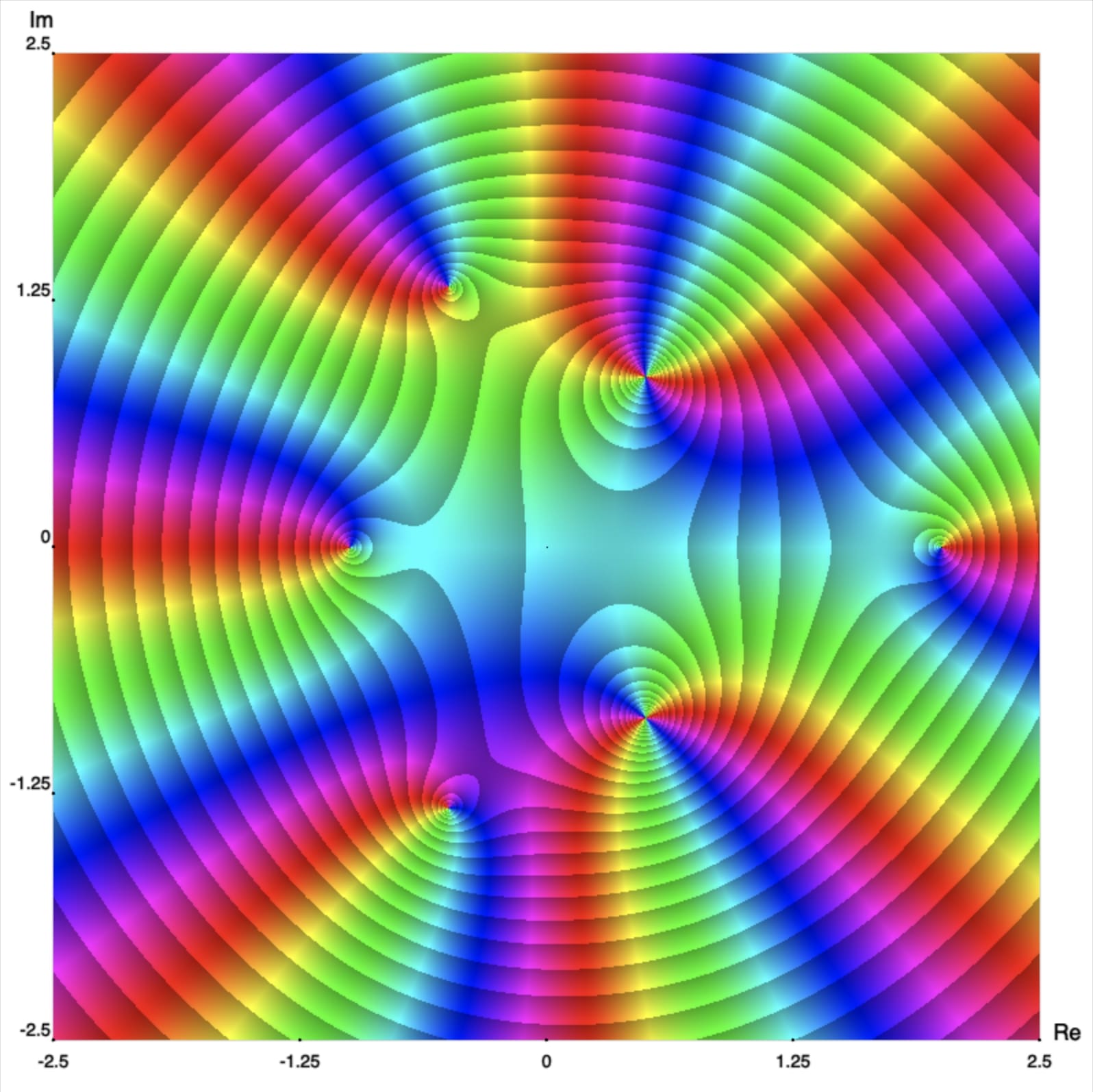
Figure 1 shows an enhanced phase portrait, with level curves of the modulus, of the polynomial defined in (\ref{example-001}). The first thing to notice from this picture is that Fundamental Theorem of Algebra does, indeed, hold for $p(z).$ Recall that we can easly spot the roots, or zeros, of complex functions using enhanced phase portraits. We just need to look at the points where all the colors meet. In Figure 1 we can clearly see that there are six points where all the colors meet, which means that $p(z)$ has 6 roots. Why does $p(z),$ a polynomial of degree eight, have only six roots? The reason is that two of the roots are double roots (we also say that its multiplicy is two), and this fact is also evident in the picture. The single roots occur at \[ -1, \;\; 2, \;\; \frac{-1\pm i \sqrt{7}}{2}, \] and the double roots are at \[ \frac{1\pm i \sqrt{3}}{2}. \] The following applet shows all the roots. Furthermore, you can appreciate their multiplicity, which is indicated by the number of times the colors repeat. For example, for the double roots, the hue colors repeat twice, whereas at the single roots they repeat only once. Activate the check boxes to highlight the roots.


Another fascinating property of the polynomial $p(z)$ can be visualized as follows. Consider a circle centered at the origin with radius $r,$ chosen such that all the roots of $p(z)$ lie inside this circle. When this circle is mapped by $p(z),$ its image becomes a closed curve that wraps around the origin exactly eight times. This behavior is illustrated in the applet below. On the left, the roots of $p(z) $ and the circle are displayed. On the right, you can see the corresponding image of the circle, clearly showing the wrapping effect. Just drag the slider below.


Proof & historical notes

Cauchy's inequality can be used to show the following result, named after the French mathematician Joseph Liouville:

(Liouville's Theorem) The only bounded entire functions are constants.
Suppose $f$ is entire and bounded, that is, $\abs{f(z)}\lt M$ for all $z.$ Then for any point $z_0,$ Cauchy's inequality gives \[ \abs{f'(z)}\leq \frac{M_r}{r}. \] By making $r$ arbitrarily large, we can make $\abs{f'(z)}$ as small as we wish. This means that $f'(z_0)= 0$ for all points $z_0$ in the complex plane. Hence, by Theorem 3 in the Complex Differentiation section, $f$ must be constant.

Now with the help of Liouville's Theorem, we can easily prove:

(Fundamental Theorem of Algebra) Any polynomial \[ p(z)= a_n z^n+ a_{n-1}z^{n-1}+\cdots + a_1z+ a_0\quad (a_n\neq 0) \] of degree $n\geq 1$ has at least one zero.
We establish this statement by contradiction. Suppose that $p(z)$ is not zero for any value of $z,$ then \[ f(z) = \frac{1}{p(z)} \] is an entire function. Since $\abs{p(z)}\to \infty$ as $\abs{z}\to \infty,$ there exists $M,$ $R\gt 0$ such that $\abs{p(z)}\gt M$ if $\abs{z}\gt R.$ This implies that for $\abs{z}\gt R,$ \[ \abs{f(z)} = \abs{\frac{1}{p(z)}} \lt \frac{1}{M}. \] Now, $f$ is continuous on the region $\abs{z}\leq R,$ which is closed and bounded. By Theorem 3, in the Continuity section, $f$ is also bounded for $\abs{z}\leq R.$ Hence $f(z)$ is bounded in the entire complex plane. Liouville's Theorem then implies that $f(z)$ is a constant, and consequently $p(z)$ is a constant as well. But this is a contradiction. We conclude that there must exist at least one number $z$ for which $p(z) = 0.$

It follows in the usual way that any polynomial $p(z)$ of degree $n,$ with complex coefficients, can be expressed as a product of linear terms: \begin{eqnarray}\label{factorized} p(z) = c\left(z-\alpha_1\right)\left(z-\alpha_2\right)\cdots \left(z-\alpha_n\right), \end{eqnarray} where $c$ and $\alpha_k$ $(k=1,2,\ldots, n)$ are complex constants. Of course, some of the constants $\alpha_k$ in expression (\ref{factorized}) may appear more than once, and it is clear that $p(z)$ cannot have more than $n$ distinct zeros.

According to B. Fine & G. Rosenberger [7, Chapter 1], the Fundamental Theorem of Algebra was first mentioned by Peter Roth of Nuremberg in 1608. However, it is also attributed to Albert Girard, who articulated the result in 1629. René Descartes later provided a clearer formulation in 1637, distinguishing between real and imaginary roots. The first published proof of the theorem came from Jean le Rond d'Alembert in 1746, though it contained significant gaps. The first widely accepted proof was presented by Carl Friedrich Gauss in his 1797 Ph.D. thesis, published in 1799 [8]. Interestingly, modern scholars note that Gauss's original proof has as many gaps as d'Alembert's (see for example [12, 14]). Nonetheless, Gauss went on to produce three more rigorous proofs: two published in 1816 and a final version, essentially a refinement of his first proof, presented in 1849 [9].

Outline of Gauss' original proof: Since $p(z)$ is a complex numbers for any $z\in \C$ and since $z=x+iy$ with $x,y\in \R$ we have that \[ p(z) = u(x,y) + i v(x,y). \] The equations $u(x,y)=0$ and $v(x,y)=0$ then represent curves in the plane $\R^2.$ By careful examination of the possible functions $u(x,y),$ $v(x,y)$ for a complex polynomial $p(z),$ Gauss showed that the curves $u(x,y)=0,$ $v(x,y)=0$ must have a common solution $(x_0, y_0).$ The complex number $z_0= x_0+iy_0$ is then the root of $p(z).$

For example, Figure 2 shows the curves $u(x,y)=0$ and $v(x,y)=0$ for the our initial polynomial $p(z) = z^8-2z^7+2z^6-4z^5+2z^4-2z^3-5z^2+4z-4.$

Real and imaginary components of a polynomial
The curves $u(x,y)=0$ (Red) and $v(x,y)=0$ (Blue) of $p(z).$ The roots are represented with the points $Z_k$.

Although it is argued that Gauss' first proofs of the Fundamental Theorem of Algebra also included some gaps, they still show an intuitive way why any complex polynomial should have a root. Nowadays there are many known proofs of this theorem, including proofs using methods of abstract algebra, analysis, and topology. The references include many papers and books containing proofs of this theorem, for example [7] alone contains 11 proofs.


References

  1. Abian, A. (1986). A new proof of the fundamental theorem of algebra, Caribbean J. Math. 5, no. 1, 9-12.
  2. Bennish, J. (1992). Another proof of the fundamental theorem of algebra, Amer. Math. Monthly, 99, 426.
  3. Boas, Jr., R. P. (1935). A proof of the fundamental theorem of algebra, Amer. Math. Monthly, 42, 501-502.
  4. Boas, Jr., R. P. (1964). Yet another proof of the fundamental theorem of algebra, Amer. Math. Monthly, 71, 180.
  5. Byl, J. (1999). A simple proof of the fundamental theorem of algebra, Internat. J. Math. Ed. Sci. Tech. 30, no. 4, 602-603.
  6. Fefferman, C. (1967). An easy proof of the fundamental theorem of algebra, Amer. Math. Monthly, 74, 854-855.
  7. Fine, B. & Rosenberger. G. (1997). The Fundamental Theorem of Algebra. New York: Springer-Verlag Inc.
  8. Gauss, C. F. (1799). Demonstratio nova theorematis omnem functionem algebraicum rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse, Helmstedt dissertation, reprinted in Werke, Vol. 3, 1-30.
  9. Gauss, C. F. (1850). Beiträge zur Theorie der algebraischen Gleichungen". Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 4: 34-35.
  10. Redheffer, R. M. (1964). What! Another note just on the fundamental theorem of algebra? Amer. Math. Monthly, 71, 180-185.
  11. Sen, A. (2000). Fundamental theorem of algebra—yet another proof, Amer. Math. Monthly, 107, 842-843.
  12. Stillwell, J. (1989). Mathematics and its History. New York: Springer-Verlag.
  13. Velleman, D. J. (1997). Another proof of the fundamental theorem of algebra, Math. Mag. 70(1997), 216-217.
  14. Vellemen, D. J. (2015). The Fundamental Theorem of Algebra: A Visual Approach, The Mathematical Intelligencer, Vol. 37, pp. 12-21.

Series