Clasificación de Singularidades

La expresión \begin{eqnarray}\label{principal} \frac{b_1}{z-z_0}+\frac{b_2}{(z-z_0)^2}+\frac{b_3}{(z-z_0)^3}+\cdots \end{eqnarray} definida en las Series de Laurent, la cual involucra las potencias negativas de $z - z_0$, se denomina parte principal de $f$ en el punto $z_0.$ El coeficiente $b_1$ en la ecuación (\ref{principal}), juega un papel muy importante en el análisis complejo. Se le da un nombre especial: el residuo de $f(z).$ En esta sección nos enfocaremos en la parte principal para identificar singulares aisladas $z_0$ en tres tipos especiales.

Polos

Si la parte principal de $f$ en $z_0$ contiene al menos un término diferente de cero pero el número de estos términos es finito, entonces existe un número entero $m \geq 1$ tal que $$b_m\neq 0 \quad\text{and} \quad b_{k}=0\quad \text{for}\quad k\gt m.$$ En este caso, la singularidad aislada $z_0$ se denomina polo de orden $m.$ Un polo de orden $m = 1$ es conocido como pole simple.

Ejemplos

Consideremos las funciones

$$f(z)=\dfrac{e^z-1}{z^2},\qquad g(z)=\frac{\cos z}{z^2}\qquad\text{and}\qquad h(z)=\frac{\sinh z}{z^4},$$

con una singularidad aislada en $z_0=0.$ Las Figuras 1, 2 y 3 muestran los retratos fase mejorados de estas funciones definidos en el cuadrado $|\text{Re }z|\lt 3$ and $|\text{Im }z|\lt 3.$

Pole order 1 — $f(z)=\dfrac{e^z-1}{z^2}.$

Pole order 2 — $g(z)=\dfrac{\cos z}{z^2}.$

Pole order 3 — $h(z)=\dfrac{\sinh z}{z^4}.$

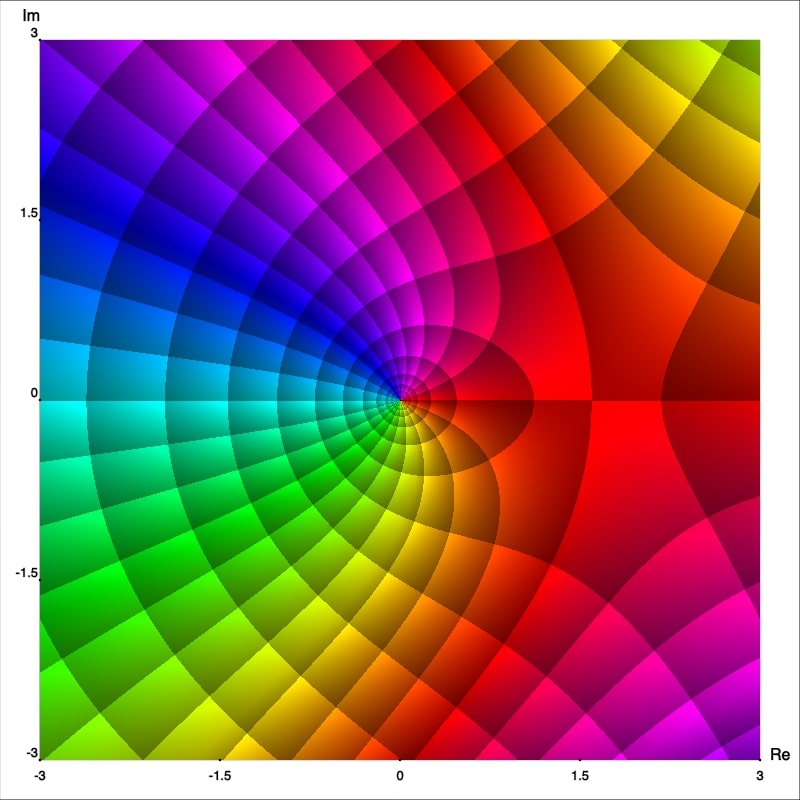
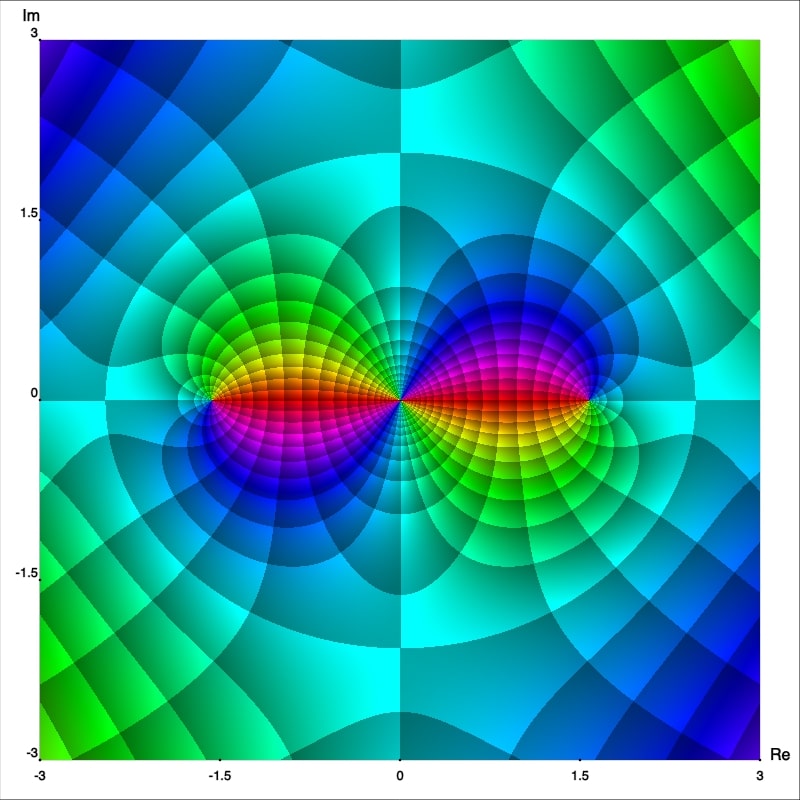
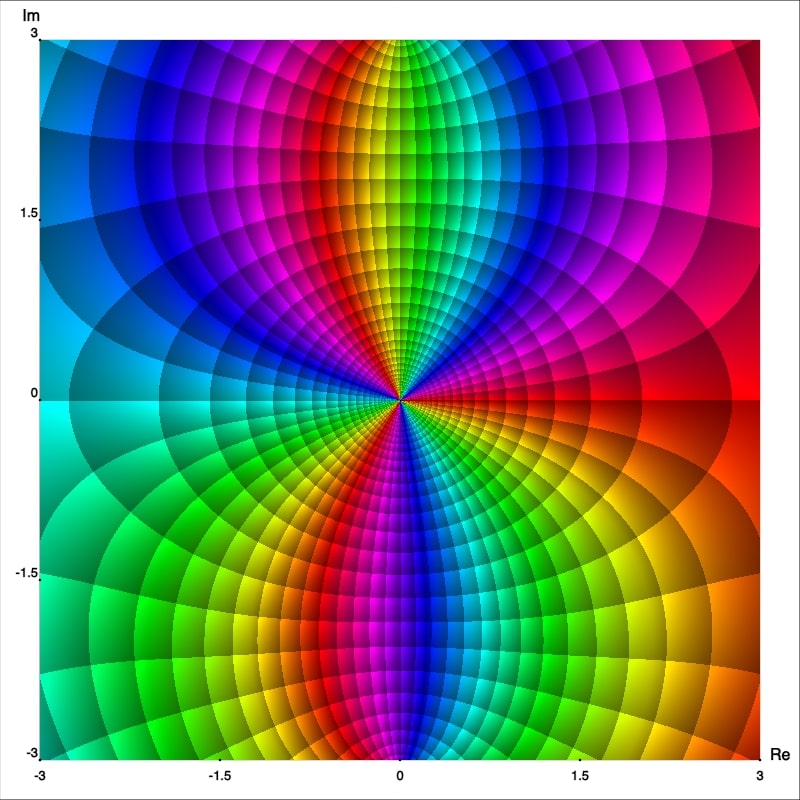
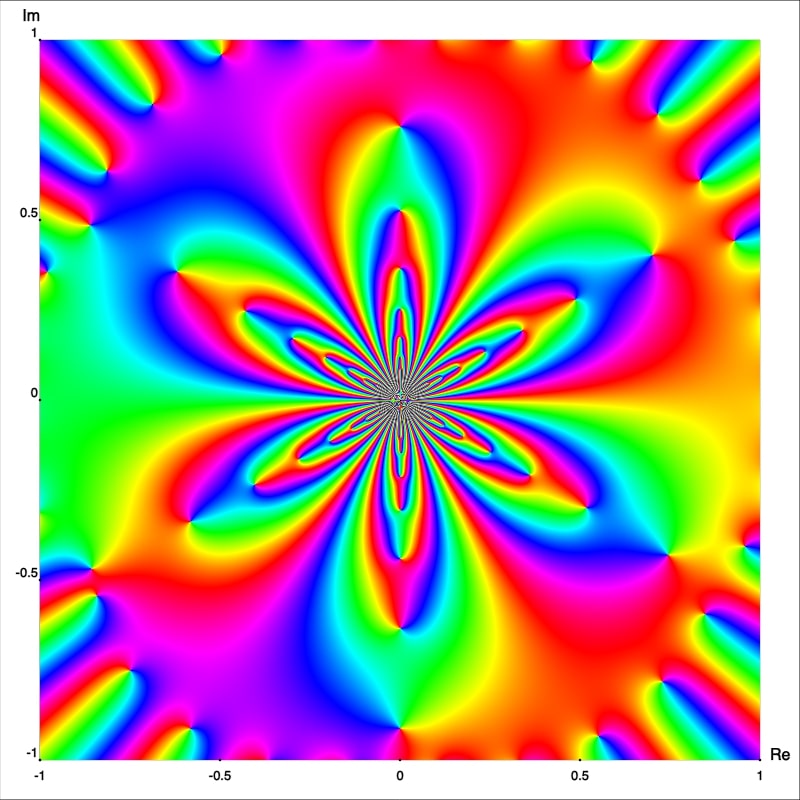
De los retratos fase mejorados podemos observar que $z_0=0$ es en realidad un polo cuyo orden se puede deducir fácilmente, este es solo el número de rayos isocromáticos de un color (arbitrariamente elegidos) los cuales se intersectan en este punto. De esta manera podemos afirmar que $f$, $g$ y $h$ tienen polo de orden 1, 2 and 3; respectivamente. Para confirmar esto calculemos las series de Laurent con centro en $0.$ Primero observemos que

\begin{eqnarray*} f(z)&=&\frac{1}{z^2}\left[ \left( 1 + z + \frac{z^2}{2!}+\cdots \right) - 1 \right]\\ &=&\frac{1}{z} +\frac{1}{2!}+\frac{z}{3!}+\frac{z^2}{4!}+\cdots, \quad (0\lt|z|\lt\infty). \end{eqnarray*}

De esta manera podemos ver que $f$ tiene un polo simple. Por otra parte

\begin{eqnarray*} g(z)&=&\frac{1}{z^2}\left(1-\frac{z^2}{2!}+\frac{z^4}{4!}-\cdots \right)\\ &=&\frac{1}{z^2}-\frac{1}{2!}+\frac{z^2}{4!}-\cdots, \quad (0\lt|z|\lt\infty) \end{eqnarray*}

entonces $g$ tiene un polo de orden 2. Finalmente, $h$ tiene un polo de orden 3 dado que

\begin{eqnarray*} h(z)&=&\frac{1}{z^4}\left(z+\frac{z^3}{3!}+\frac{z^5}{5!}+\cdots \right)\\ &=&\frac{1}{z^3}+\frac{1}{3!}\cdot \frac{1}{z}+\frac{z}{5!}+\frac{z^3}{7!}+\cdots, \quad(0\lt|z|\lt\infty). \end{eqnarray*}

Singularidad removible

Cuando cada $b_n$ es cero, tal que

\begin{eqnarray}\label{residue003} f(z)=\sum_{n=0}^{\infty} a_n(z-z_0)^n,\quad (0\lt |z-z_0| \lt R_2). \end{eqnarray}

En este caso, $z_0$ se conoce como singularidad removible. Notemos que el residuo en una singularidad removible es siempre cero. Si definimos, po posiblemente redefinimos, $f$ en $z_0$ como $f(z_0) = a_0$, la expansión (\ref{residue003}) se vuelve válida en todo el disco $|z - z_0| \lt R_2.$ Dado que una serie de potencias siempre representa una función analítica interior a este disco de convergencia, se sigue que $f$ es analítica en $z_0$ cuando se le asigna el valor de $a_0.$ La singularidad $z_0$ es, por lo tanto, removida.

Ejemplos

Consideremos las funciones

$$f(z)=\frac{1-\cos z}{z^2},\qquad g(z)=\frac{\sin z}{z}\qquad\text{and}\qquad h(z)=\frac{z}{e^z-1}.$$

Las Figuras 4, 5 y 6 muestran los retratos fase mejorados de estas funciones definidas en $|\text{Re }z|\lt 8$ and $|\text{Im }z|\lt 8.$

Removable singularity — $f(z)=\dfrac{1-\cos z}{z^2}.$

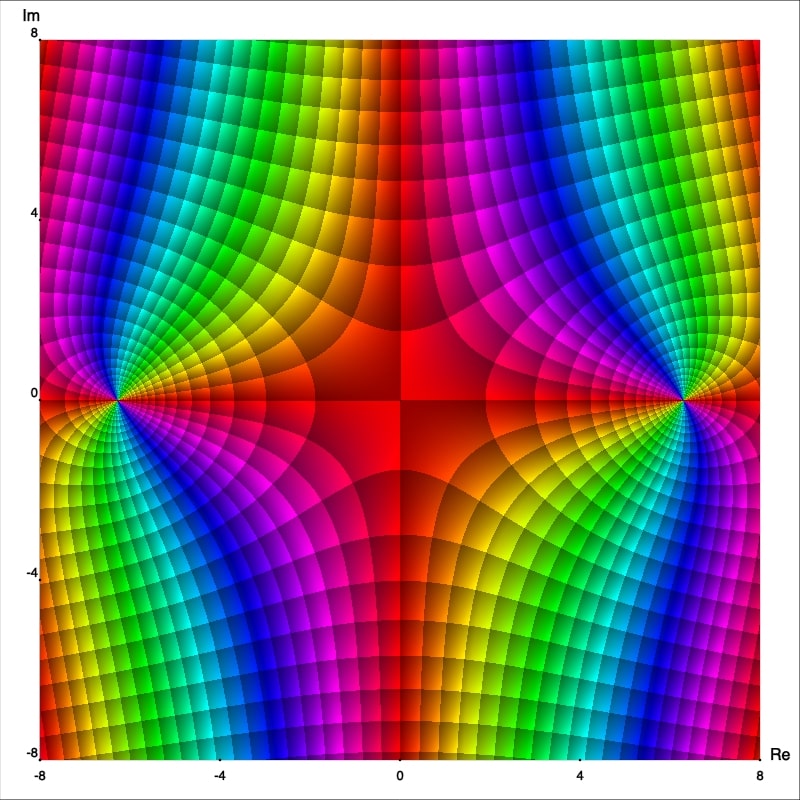
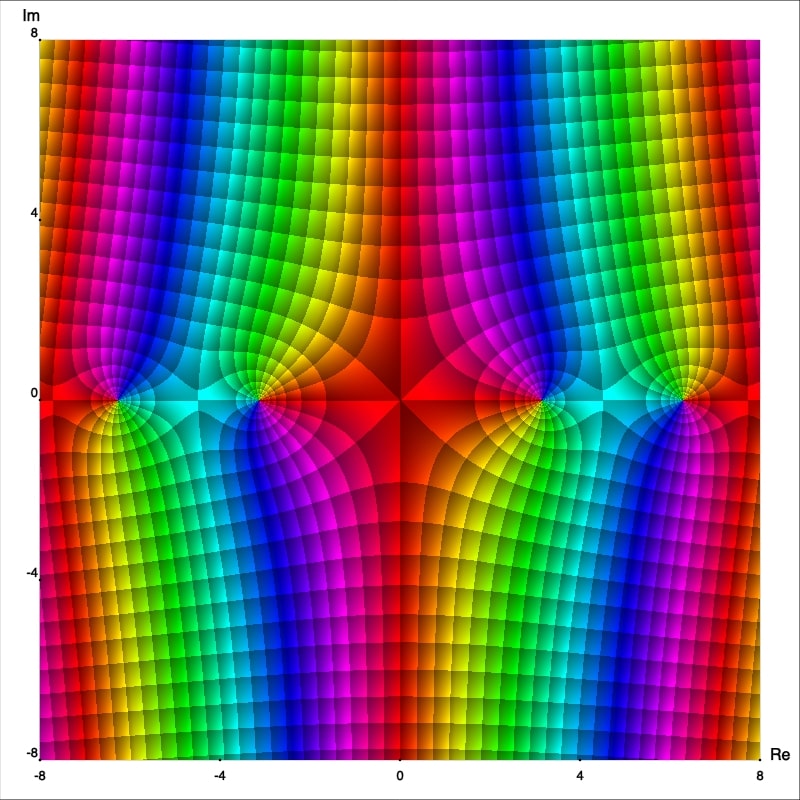
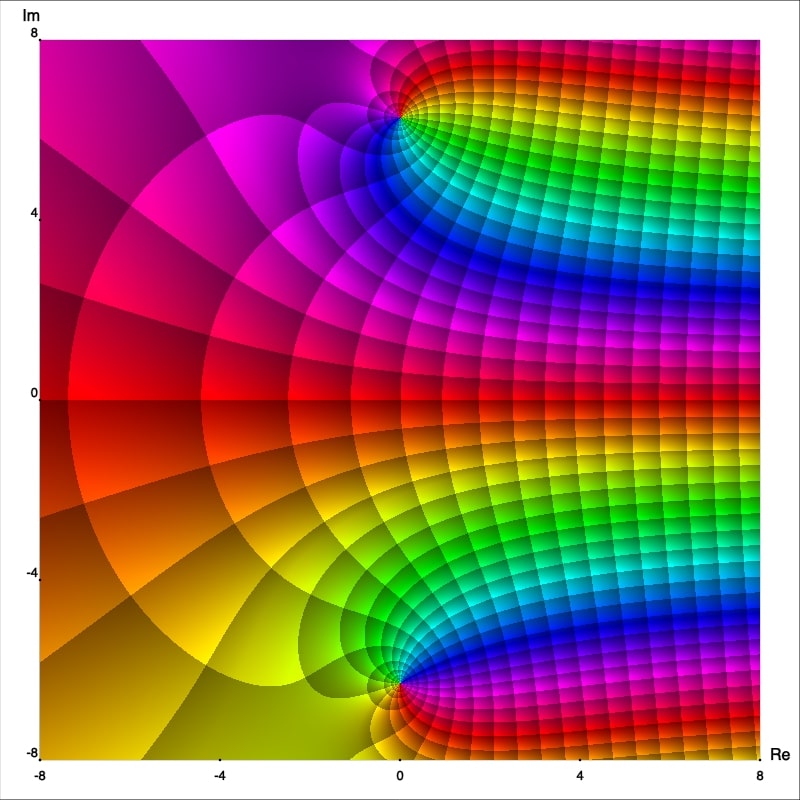
Notemos que $f$ tiene una singularidad en $z_0=0$ pero en este caso la gráfica no muestra líneas isocromáticas intersectándose en un punto. Esto indica que la singularidad es removible.

Podemos confirmar esto fácilmente de la representación en series de Laurent: \begin{eqnarray*} f(z)&=&\frac{1}{z^2}\left[1-\left(1-\frac{z^2}{2!}+\frac{z^4}{4!}-\frac{z^6}{6!}+\cdots \right)\right]\\ &=&\frac{1}{2!}-\frac{z^2}{4!}+\frac{z^4}{6!}-\cdots, \quad (0\lt |z|\lt \infty). \end{eqnarray*} En este caso, cuando se asigna el valor $f(0)=1/2$, $f$ se vuele entera. Más aún, podemos observar intuitivamente dado que $z=0$ es una singularidad removible de $f$, entonces $f$ debe ser analítica y acotada en alguna vecindad borrada (perforada) $0\lt |z|\lt \varepsilon.$

Ejercicio 1: Calcula las series de Laurent de las funciones $g$ y $h$ para confirmar que tienen singularidades removibles en $z_0=0.$

Singularidad esencial

Si un número infinito de coeficientes $b_n$ en la parte principal (\ref{principal}) son diferentes de cero, entonces $z_0$ se conoce como una singularidad esencial de $f.$

Ejemplos

La función $$f(z)=\exp\left(\frac{1}{z}\right)$$ tiene una singularidad esencial en $z_0=0$ dado que \begin{eqnarray*} f(z)&=&1+\frac{1}{1!}\cdot\frac{1}{z}+\frac{1}{2!}\cdot \frac{1}{z^2}+\cdots\\ &=&\sum_{n=0}^{\infty}\frac{1}{n!}\cdot \frac{1}{z^n}, \quad (0\lt |z|\lt \infty). \end{eqnarray*}

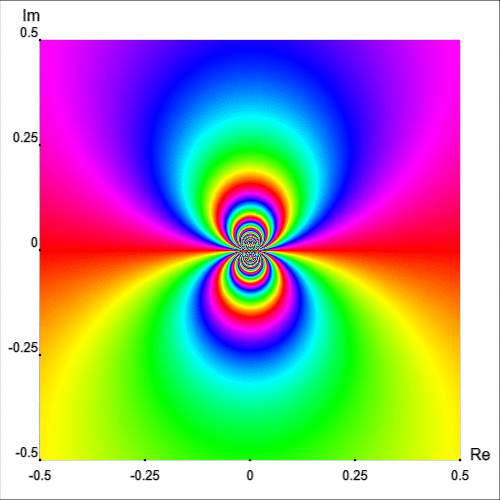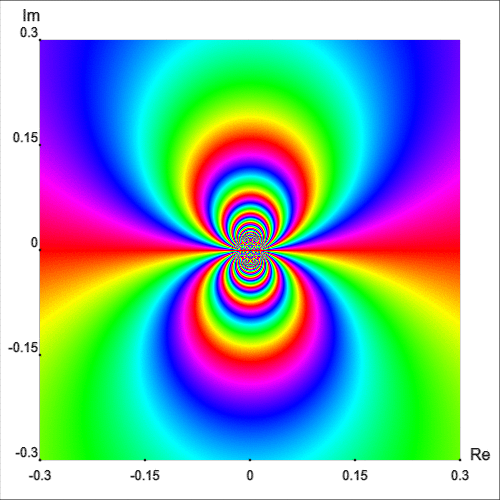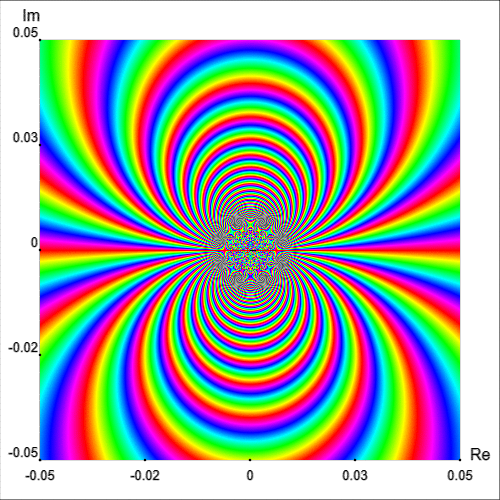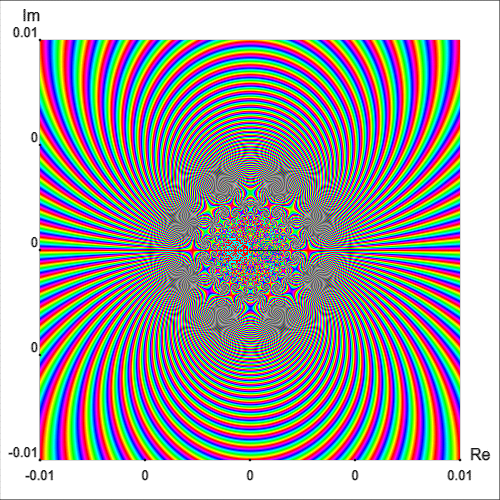
La Figura 7 muestra el retrato mejorad de $f$ en el cuadrado ${|\text{Re }z|\lt 0.5}$ and ${|\text{Im }z|\lt 0.5}.$ Lo primero que notamos de este gráfico es el comportamiento de $f$ cerca de la singularidad esencial el cual es bastante irregular. Observemos como las líneas isocromáticas, cerca de $z_0=0$, forman figuras con forma de ocho auto contenidas.

Essential singularity — $\exp(1/z)$ definida en $[-0.5, 0.5]\times[-0.5, 0.5].$

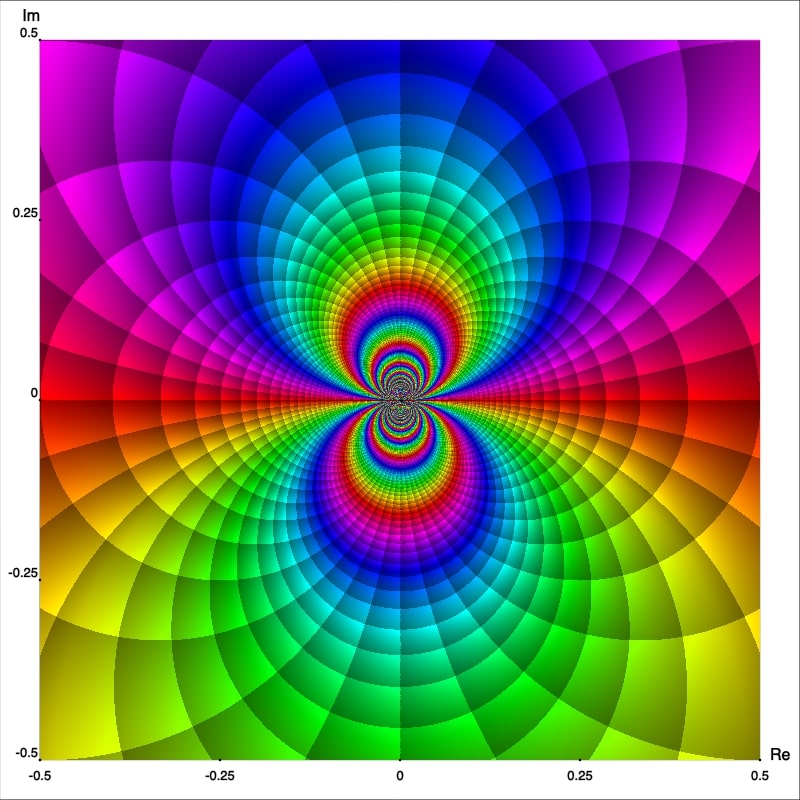
En realidad, una vecindad de $z_0=0$ intersecta infinitamente muchas líneas isocromáticas del retrato fase de un y del mismo color [Wegert, 2012, p. 181]. Este hecho se puede apreciar mejor con el retrato fase simple de $\exp(1/z)$ en una región cercana al origen, como se muestra en la Figura 8.

Otro ejemplo con una singularidad esencial en el origen es la función $$g(z) = (z - 1) \cos\left(\frac{1}{z}\right)$$ La Figura 9 muestra el retrato fase de $g$ en el cuadrado $|\text{Re } z| \lt 0.3$ y $|\text{Im } z| \lt 0.3.$

Ejercicio 2: Calcula la serie de Laurente de $(z - 1) \cos(1/z)$ para confirmar que $z_0=0$ es una singularidad esencial.

Comentario final

Los retratos de fase son bastante útiles para comprender el comportamiento de funciones complejas cerca de singularidades aisladas. Las Figuras 7 y 9 indican un comportamiento bastante radical de estas funciones en una vecindad con singularidades esenciales, en comparación con polos y singulares removibles. Además, se pueden utilizar para explorar y comprender, desde un punto de vista geométrico, resultados matemáticos más abstractos como el Gran Teorema de Picard, el cual nos dice que cualquier función analítica con una singularidad esencial en $z_0$ toma todos los posibles valores complejos (con una sola excepción como máximo) infinitamente a menudo en cualquier vecindad de $z_0.