Curvas en el Plano Complejo

---

Supongamos que las funciones de valor real $x = x(t),$ $y = y(t),$ $a \leq t \leq b,$ son ecuaciones paramétricas de una curva $C$ en el plano complejo. Si usamos estas ecuaciones como las partes reales e imaginarias en $z = x+iy,$ podemos describir los puntos $z$ en $C$ por medio de la función de valor complejo de una variable real $t.$ Esto determina una parametrización de $C$: \begin{equation}\label{parcurve} z(t) = x(t) + i y(t), \quad a\leq t\leq b. \end{equation}

El punto $z(a) = x(a) + i y(a)$ ó $z_0 = (x(a), y(a))$ se denomina como punto inicial de $C$ y $z(b) = x(b) + iy(b)$ o $z_1 = (x(b), y(b))$ es el punto final. La expresión $z(t) = x(t) + iy(t)$ se puede interpretar como una función vectorial de dos dimensiones. Consecuentemente, $z(a)$ y $z(b)$ se pueden interpretar como los vectores posición. Así que cuando $t$ varía desde $t = a$ a $t = b$ podemos observar la curva $C$ trazada por el movimiento de la punta del vector $z(t).$ Esto se puede apreciar en el siguiente applet con $0 \leq t\leq 1.$

Clic Start para animar. También puedes mover los puntos para cambiar la curva.

Por ejemplo, las ecuaciones paramétricas $x = \cos t,$ $y = \,\text{sen } t,$ $0 \leq t \leq 2\pi,$ describen un círculo de radio unitario con centro en el origen. Una parametrización de este círculo es $z(t) = \cos t + i \,\text{sen } t,$ o $z(t) = e^{it},$ $0 \leq t \leq 2\pi.$

Clic Start para animar.

Contornos

Las nociones de curvas en el plano complejo que son suaves, suaves por piezas, simple, cerradas, y simplemente cerradas, se pueden formular fácilmente en términos de la función vectorial (\ref{parcurve}). Supongamos que la derivada de (\ref{parcurve}) es $z'(t) = x'(t) + iy'(t).$ Decimos que una curva $C$ en el plano complejo es suave si $z'(t)$ es continua y diferente de cero en el intervalo $a \leq t \leq b.$ Como se muestra en la Figura 1, dado que el vector $z'(t)$ no es cero en ningún punto $P$ de $C,$ el vector $z'(t)$ es tangente a $C$ en $P.$ De esta forma, una curva suave tiene una tangente que gira continuamente; o en otras palabras, una curva suave no puede tener esquinas ni cúspides afiladas, como se muestra en la Figura 2.

Una curva suave por piezas $C$ tiene una tangente que gira continuamente, excepto posiblemente en los puntos donde las componentes de las curvas suaves $C_1, C_2, \ldots, C_n$ se conectan.

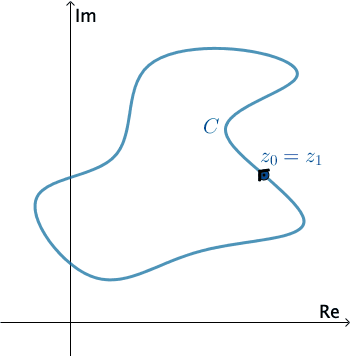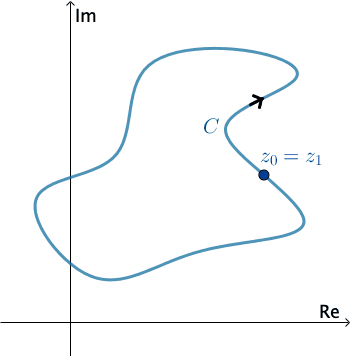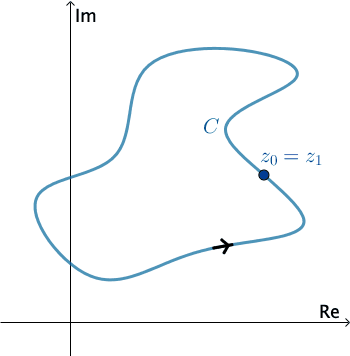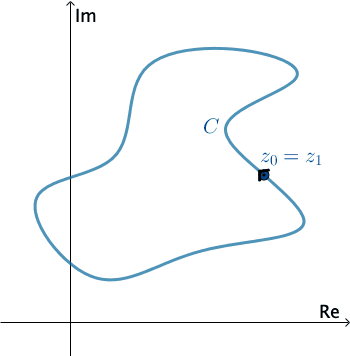
Una curva $C$ en el plano complejo se dice ser simple si $z(t_1) \neq z(t_2)$ para $t_1 \neq t_2,$ excepto posiblemente para $t = a$ y $t = b.$ $C$ es una curva cerrada si $z(a) = z(b).$

$C$ es una curva cerrada simple si $z(t_1)\neq z(t_2)$ para $t_1\neq t_2$ y $z(a) = z(b).$

En Análisis Complejo, una curva suave por piezas $C$ se denomina contorno o camino. Definimos la dirección positiva en un contorno $C$ como la dirección en la curva correspondiente a los valores incrementados del parámetro $t.$ También decimos que la curva $C$ tiene una orientación positiva. En el caso de un contorno cerrado simple $C,$ la dirección positiva corresponde a la dirección del movimiento opuesto a las manecillas del reloj. Por ejemplo, el círculo $z(t) = e^{it},$ $0 \leq t \leq 2\pi,$ tiene una orientación positiva. La dirección negativa de un contorno $C$ es la dirección opuesta a la dirección positiva. Si $C$ tiene una orientación, la curva opuesta, es decir, una curva con orientación opuesta, se denota como $−C.$ En una curva cerrada simple, la dirección opuesta corresponde al movimiento de las manecillas del reloj. Por ejemplo, el círculo $z(t) = e^{-it},$ $0 \leq t \leq 2\pi,$ tiene una orientación negativa.

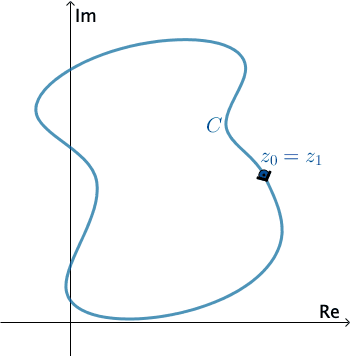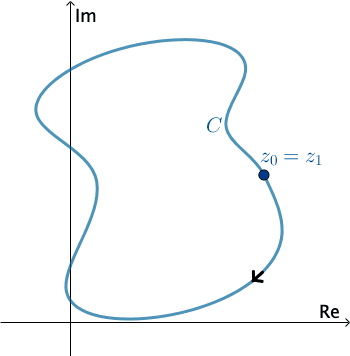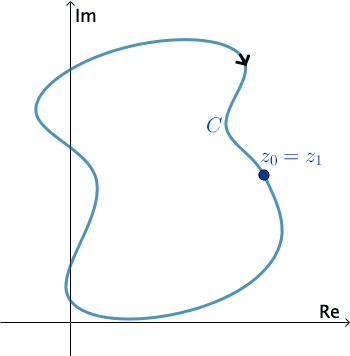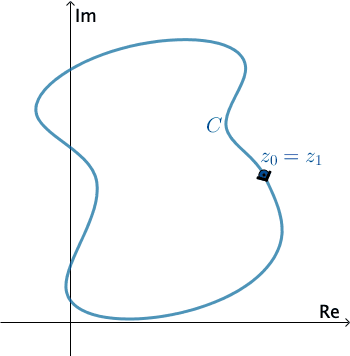
Clic Start para animar. También puedes cambiar la dirección de $C.$