Integración Compleja

Integral de Contorno

Consideremos un contorno $C$ parametrizado por $z(t) = x(t) + i y(t)$ con $a\leq t\leq b.$ Definimos la integral de la función compleja a lo largo de $C$ como el número complejo \begin{eqnarray}\label{contour-integral} \int_C f(z)\,dz = \int_a^bf\left(z(t)\right)z'(t)\,dt. \end{eqnarray} Aquí asumiremos que $f\left(z(t)\right)$ es continua por piezas en el intervalo $a \leq t \leq b$ y nos referimos a la función $f (z)$ como continua por piezas en $C.$ Dado que $C$ es un contorno, $z'(t)$ es también continuo por piezas en $a \leq t \leq b$; y esto garantiza la existencia de la integral (\ref{contour-integral}).

El lado derecho de (\ref{contour-integral}) es una integral real ordinaria de una función compleja; es decir, si $w(t) = u(t) + i v(t),$ entonces \begin{eqnarray}\label{integral-real-cv} \int_a^b w(t)\,dt = \int_a^b u(t)\,dt + i \int_a^b v(t)\,dt. \end{eqnarray}

Ahora escribamos el integrando $$f(z)= u(x,y)+ iv(x,y)$$ en términos de sus componentes real e imaginaria, así como su diferencial $$dz=\frac{dz}{dt}dt = \left(\frac{dx}{dt}+ i \frac{dy}{dt}\right)dt = dx+ i dy$$ Entonces la integral compleja (\ref{contour-integral}) se divide en un par de integrales reales:

Ejemplo 1: Vamos a evaluar la integral $\int_C \overline{z}\, dz,$ donde $C$ está dado por las ecuaciones paramétricas $x=3t, y=t^2,$ con $-1\leq t\leq 4.$

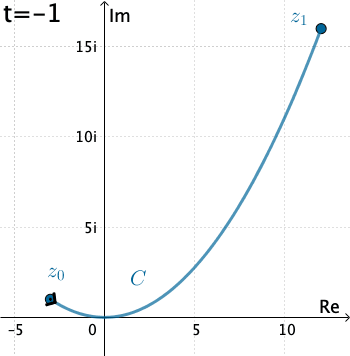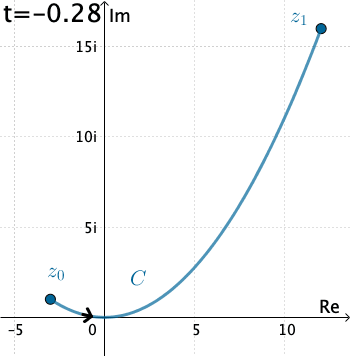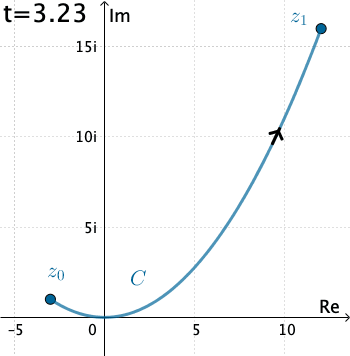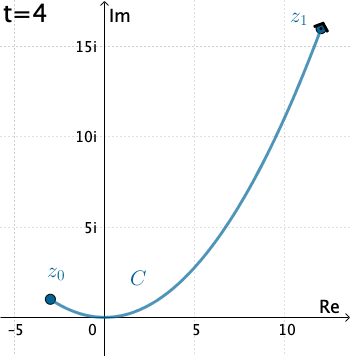
Aquí tenemos que $C$ está definido como $z(t)=3t+ it^2 .$ Por lo tanto, con la identificación $f(z)=\overline{z}$ tenemos $$f\left(z(t)\right)=\overline{3t+it^2}= 3t-it^2 .$$ Mientras que $z'(t) = 3 + 2it,$ y así la integral es \begin{eqnarray*} \int_C \overline{z}\, dz&=& \int_{-1}^4 \left(3t-it^2\right)\left(3+ 2it\right)dt\\ &=& \int_{-1}^4 \left(2t^3+9t + 3t^2i\right)dt\\ &=& \int_{-1}^4 \left(2t^3+9t \right)dt + i\int_{-1}^4 3t^2dt\\ &=& \Bigg. \left(\frac{1}{2}t^4 + \frac{9}{2} t^2\right)\Bigg|_{-1}^4 + i\Bigg. t^3\Bigg|_{-1}^4\\ &=& 195+ 65 i. \end{eqnarray*}

Ejemplo 2: Ahora evaluemos la integral $\displaystyle \int_C \dfrac{1}{z}\, dz,$ donde $C$ es el círculo $x=\cos t, y=\sin t,$ con $0\leq t\leq 2\pi .$

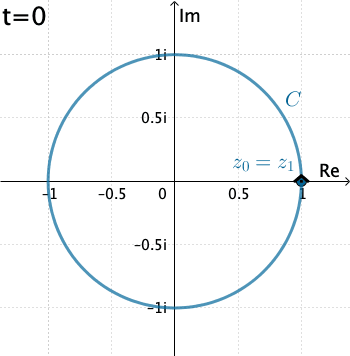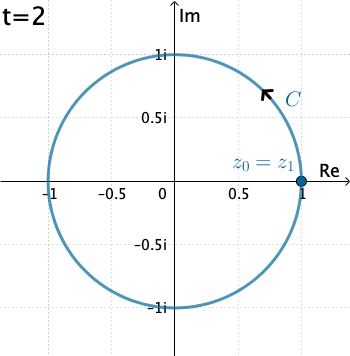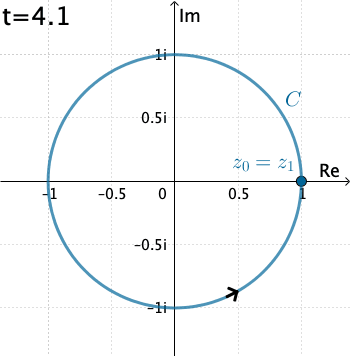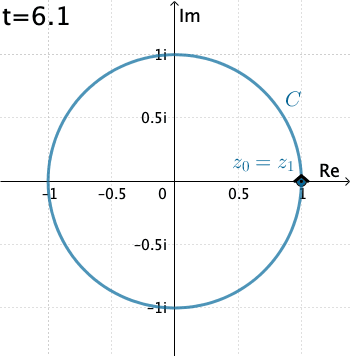
En este caso $C$ es $z(t)=\cos t + i\,\text{sen }t = e^{it}.$ Entonces $$f\left(z(t)\right)=\frac{1}{e^{it}}\quad \text{ y }\quad z'(t) = ie^{it}.$$ De esta manera \begin{eqnarray*} \int_C \dfrac{1}{z}\, dz&=& \int_{0}^{2\pi} \left(e^{-it}\right)ie^{it}dt = i \int_{0}^{2\pi} dt= 2\pi \,i. \end{eqnarray*}

Evaluación numérica de integrales complejas

Exploración 1

Usa el siguiente applet para explorar numéricamente la integral $$\int_C \overline{z}\, dz$$ con diferentes contornos $C$:

• Segmentos de línea.
• Semicírculos.
• Círculos, con orientación positiva y negativa.

También puedes cambiar la opción de domain coloring. Mueve los puntos y observa con cuidado lo que sucede. Después resuelve el Ejercicio 1 propuesto abajo.

Las flechas en los contornos indican la dirección.

Exploración 2

Ahora usa el applet siguiente para explorar numéricamente la integral $$\int_C \left(z^2+z\right) dz;\qquad \int_C \frac{1}{z^2}\, dz$$ con diferentes contornos $C$ (segmentos de línea, semicírculos y círculos). Mueve los puntos y observa con cuidad lo que sucede. Puedes seleccionar las funciones z^2+z ó 1/z^2 de la lista en la esquina superior izquierda. Después resuelve los Ejercicios 2 y 3.

Propiedades

Todas las siguientes propiedades conocidas de las integrales pueden ser probadas directamente a partir de la definición dada en (\ref{integral-real-cv}). Si \( w(t) = u(t) + iv(t) \) y \( s(t) = \upsilon(t) + i\nu(t) \) son funciones de valor complejo de una variable real \( t \) continuas en un intervalo \([a,b],\) entonces:

De la definición (\ref{contour-integral}) y las propiedades mencionadas anteriormente, se sigue inmediatamente que:

Ahora consideremos el contorno definido para la integral (\ref{contour-integral}). El contorno $-C$ consiste en el mismo conjunto de puntos pero con el orden invertido, de modo que el nuevo contorno se extiende desde $z_2$ hasta $z_1,$ como se muestra en la Figura 3.

El contorno $-C$ tiene una representación paramétrica $z = z(-t)$ con $-b \leq t \leq -a.$ Por lo tanto,

Si utilizamos la sustitución $\tau = -t$ en la última integral, entonces:

Por lo tanto, obtenemos la siguiente propiedad

Consideremos ahora un camino $C,$ parametrizado por $z(t)$ para $t \in [a,b],$ que consiste en un contorno $C_1$ desde $z_1$ hasta $z_2$ seguido por un contorno $C_2$ desde $z_2$ hasta $z_3,$ siendo el punto inicial de $C_2$ el punto final de $C_1.$ Entonces

Finalmente, introducimos una desigualdad que involucra integrales de contorno, la cual es de suma importancia en varias aplicaciones. Consideremos $C$ una curva suave parametrizada por $z(t) = x(t) + iy(t)$ con $t \in [a,b].$ Supongamos que las componentes $x'(t)$ y $y'(t)$ de la derivada \[ z'(t) = x'(t) + iy'(t) \] son continuas en todo el intervalo $[a,b].$ Entonces, la función real \[ \left|z'(t)\right| = \sqrt{\left[x'(t)\right]^2 + \left[y'(t)\right]^2} \] es integrable en $[a,b].$ Según la definición de longitud de arco de cálculo, la longitud de $C$ es el número \[ L = \int_a^b \left|z'(t)\right|\,dt. \]

Si $C$ es un contorno de longitud $L$ y $f$ es una función por tramos continua en $C$, y $M$ es una constante no negativa tal que $\left|f(z)\right|\leq M$ para todos los puntos $z$ en $C$ donde $f(z)$ está definida, entonces \begin{eqnarray}\label{ML-inequality} \left|\int_C f(z)\, dz\right|\leq ML \end{eqnarray}

Dado que $C$ es un contorno y $f$ es una función por tramos continua en $C$, siempre existirá un número $M$ que aparece en la desigualdad $\left|f(z)\right|\leq M$. La razón es que la función de valor real $\left|f\big(z(t)\big)\right|$ es continua en el intervalo cerrado y acotado $[a,b]$ cuando $f$ es continua en $C$; y esta función siempre alcanza un valor máximo $M$ en ese intervalo. Por lo tanto, $|f(z)|$ tiene un valor máximo en $C$ cuando $f$ es continua en él. Esto también es cierto cuando $f$ es por tramos continua en $C$.

La propiedad (\ref{ML-inequality}) se utiliza frecuentemente en la teoría de la integración compleja y a veces se conoce como la desigualdad ML.

Ejemplo 3: Sea $C$ el contorno del círculo $|z|=2$ desde $z_1=2$ hasta $z_2=2i$ que se encuentra en el primer cuadrante, como se muestra en la Figura 5. Podemos usar la desigualdad (\ref{ML-inequality}) para demostrar que \[ \left|\int_C \frac{dz}{z^2-1}\right|\leq \frac{\pi}{3}. \] sin evaluar la integral.

Observa que si $z$ es un punto de $C,$ entonces

\begin{eqnarray*} \left|z^2-1\right|\geq \left|\left|z^2\right|- 1\right|= \left|\left|z\right|^2- 1\right| = \left|4- 1\right|=3 \end{eqnarray*}

De esta manera \[ \left|\frac{1}{z^2-1}\right| = \frac{1}{ \left|z^2- 1\right|}\leq \frac{1}{3} \] Además, la longitud de $C$ es $\dfrac{1}{4}(4\pi).$ Así que, si tomamos $M=\dfrac{1}{3}$ y $L= \pi,$ encontramos que \[ \left|\int_C \frac{dz}{z^2-1}\right|\leq ML = \frac{\pi}{3}. \]

Ejemplo 4: También podemos usar la desigualdad ML para encontrar el valor de la integral \[ \lim_{R\to \infty} \int_{C_R}\frac{z^{1/2}}{z^2+1}dz \] donde \(C_R\) es el arco \(z(t) = Re^{it},\) con \(t \in [0, \pi]\) y \(z^{1/2}\) denota la rama \[ z^{1/2} = \exp\left(\frac{1}{2}\log z\right) = \sqrt{r}e^{it/2},\quad \left(r > 0, -\frac{\pi}{2} < t < \frac{3\pi}{2}\right) \] de la función raíz cuadrada.

Observa que cuando $|z|=R\gt 1,$ entonces $\abs{z^{1/2}}= \abs{\sqrt{R}e^{it/2}} = \sqrt{R}$ y \[ \abs{z^2+1}\geq \abs{\abs{z^2}-1} = R^2-1. \] De esta manera, para los puntos en $C_R$, tenemos

\[ \abs{\frac{z^{1/2}}{z^2+1}}\leq M_R \quad \text{done} \quad M_R = \frac{\sqrt{R}}{R^2-1}. \]

Dado que la longitud de $C_R$ es $L=\pi R,$ usando (\ref{ML-inequality}), tenemos que

\[ \abs{\int_{C_R}\frac{z^{1/2}}{z^2+1}dz}\leq M_R L = \frac{\pi R\sqrt{R}}{R^2-1} \cdot \frac{1/R^2}{1/R^2}= \frac{\dfrac{\pi}{\sqrt{R}}}{1 - \dfrac{1}{R^2}}. \]

El término en el lado derecho tiende a cero cuando \(R\) tiende a infinito. Por lo tanto \[ \lim_{R\to \infty} \int_{C_R}\frac{z^{1/2}}{z^2+1}dz=0. \]

Antiderivadas

Aunque el valor de una integral de contorno de una función $f (z)$ desde un punto fijo $z_0$ a otro punto fijo $z_1$ depende, en general, del camino que se toma, existen ciertas funciones cuyas integrales desde $z_0$ a $z_1$ tienen valores que son independientes del camino, como ya habrás notado en los Ejercicios 2 y 3. Estos ejemplos también ilustran el hecho de que los valores de las integrales alrededor de caminos cerrados simples son algunas veces, pero no siempre, cero. El siguiente teorema es útil para determinar cuando la integración es independiente del camino y, más aún, cuando una integral alrededor de un camino cerrado tiene un valor cero. Este teorema es conocido como la versión compleja del Teorema Fundamental del Cálculo e involucra el concepto de antiderivada (o primitiva) de una función continua \(f(z)\) en un dominio \(D,\) es decir, una función \(F(z)\) tal que \(F'(z) = f(z)\) para todo \(z \in D.\)

Como consecuencia del Teorema 1 tenemos que \begin{eqnarray} \int_{C} f\left(z\right)dz=\int_{C}F^{\prime}(z) dz=0. \end{eqnarray} para todo contorno $C,$ es decir, los puntos finales son iguales.

Si la función $f(z)$ satisface la hipótesis del Teorema 1, entonces para todo contorno $C$ en el interior de $D$ que comienza en $z_1$ y termina en $z_2$ tenemos la expresión (\ref{FTC}). Por lo tanto el resultado demuestra que la integral es independiente del camino recorrido. Este hecho se ilustra en la Figura 6.

Considerando la Figura 6, tenemos que $$\int_{C_1} f\left(z\right)dz=\int_{C_2} f\left(z\right)dz$$ porque

Además, tenemos la siguiente condición suficiente para la existencia de una antiderivada:

Consideremos la función \begin{eqnarray}\label{anti-exists} F(z) = \int_{z_0}^{z}f(s)\,ds \end{eqnarray} donde \(s\) denota una variable compleja, \(z_0\) es un punto fijo en \(D,\) y \(z\) representa cualquier punto en \(D.\) Asumiendo que \(f\) es continua y \(\ds\int_C f(z)\,dz\) es independiente del camino, queremos demostrar que \(F'(z) = f(z),\) es decir, que (\ref{anti-exists}) es una antiderivada de \(f\) en \(D.\)

Usando las propiedade de la integral tenemos

\begin{eqnarray}\label{anti-def} F(z+ \Delta z) - F(z) = \int_{z_0}^{z+\Delta z}f(s)\,ds - \int_{z_0}^{z}f(s)\,ds = \int_{z}^{z+\Delta z}f(s)\,ds. \end{eqnarray}

Dado que \(D\) es un dominio, podemos elegir \(\Delta z\) de modo que \(z + \Delta z\) esté en \(D.\) Además, \(z\) y \(z + \Delta z\) pueden unirse mediante un segmento recto, como se muestra en la Figura 7. Este es el contorno que utilizamos en la última integral en (\ref{anti-def}). Para \(z\) fijo, podemos escribir:

\begin{eqnarray}\label{anti-expand} f(z) \Delta z =f(z) \int_{z}^{z+\Delta z}ds = \int_{z}^{z+\Delta z}f(z)\,ds \quad \text{o}\quad f(z) = \frac{1}{\Delta z} \int_{z}^{z+\Delta z}f(z)\,ds. \end{eqnarray}

De la expressiones (\ref{anti-def}) y (\ref{anti-expand}) obtenemos

\begin{eqnarray*} \frac{F(z+\Delta z)-f(z)}{\Delta z} = \frac{1}{\Delta z} \int_{z}^{z+\Delta z}\left[f(s) - f(z)\right]\,ds. \end{eqnarray*}

Ahora, dado que \(f\) es continua, para cualquier \(\epsilon > 0\) existe un \(\delta > 0\) tal que \(\abs{f(s) - f(z)} \lt \epsilon\) siempre que \(\abs{s - z} \lt \delta.\) Por lo tanto, si elegimos \(z + \Delta z\) lo suficientemente cerca de \(z\) de modo que \(\abs{\Delta z} \lt \delta,\) se deduce de la desigualdad ML que

\begin{eqnarray*} \abs{\frac{F(z+\Delta z)-f(z)}{\Delta z} } &= &\abs{\frac{1}{\Delta z} \int_{z}^{z+\Delta z}\left[f(s) - f(z)\right]\,ds}\\ &=& \abs{\frac{1}{\Delta z}} \abs{ \int_{z}^{z+\Delta z}\left[f(s) - f(z)\right]\,ds}\\ &\leq & \abs{\frac{1}{\Delta z}}\epsilon \abs{\Delta z} = \epsilon. \end{eqnarray*}

Por lo tanto, hemos probado que

\begin{eqnarray*} \lim_{\Delta z \to 0}\frac{F(z+\Delta z)-f(z)}{\Delta z} = f(z)\quad \text{o}\quad F'(z) = f(z). \end{eqnarray*}