Diferenciación Compleja

La noción de derivada compleja es la base de la teoría de funciones complejas. La diferenciación compleja se define de la misma manera que en los cursos de Cálculo usando la definición de límite de la derivada de una función. Sin embargo, a pesar de su superficial similitud, la diferenciación compleja es profundamente una teoría diferente.

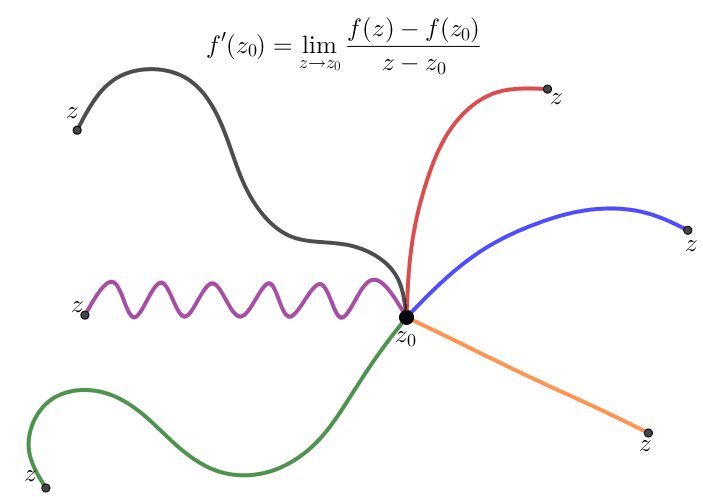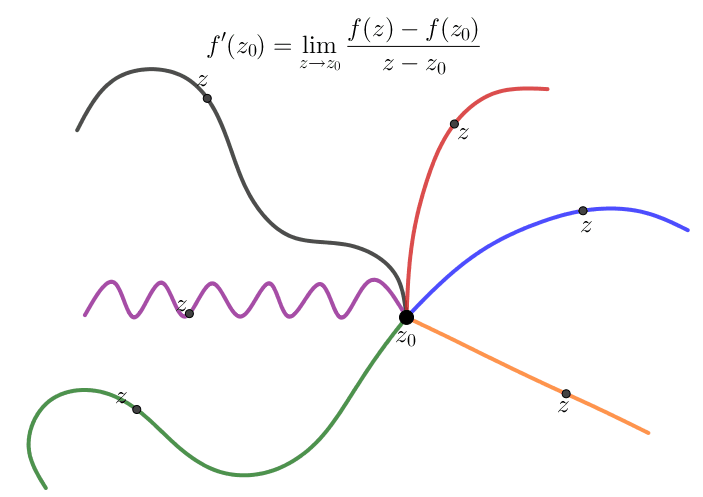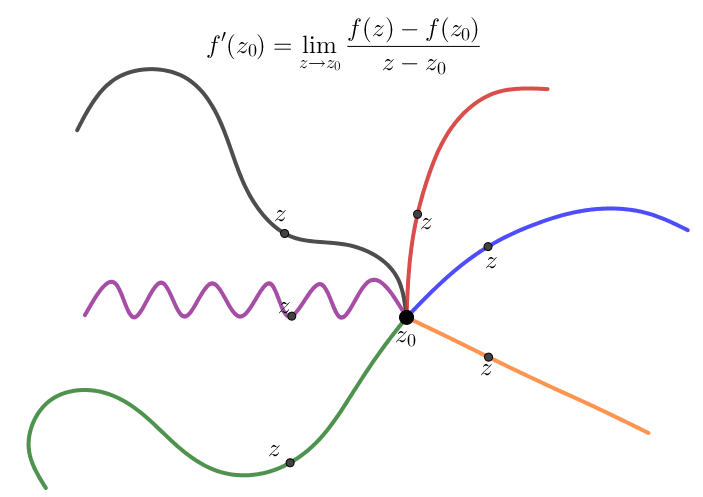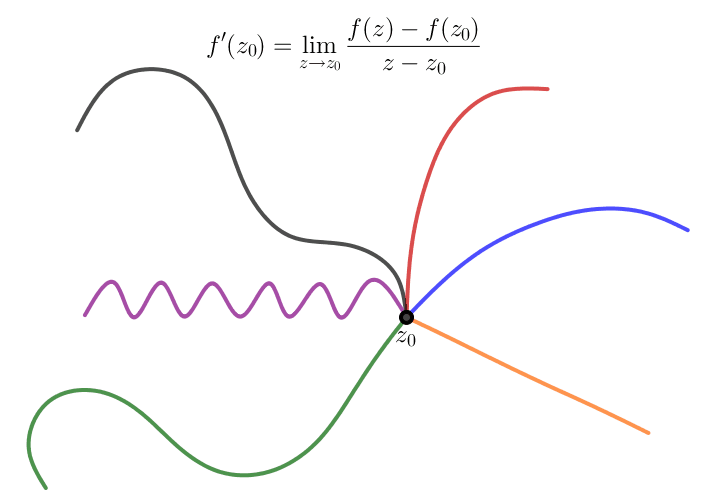
Una función compleja $f(z)$ es diferenciable en el punto $z_0\in \mathbb C$ si y solo si el siguiente límite del cociente de diferencias existe

\begin{eqnarray}\label{diff01} f'(z_0) = \lim_{z \rightarrow z_0} \frac{f(z)-f(z_0)}{z-z_0}. \end{eqnarray}

Alternativamente, definiendo $\Delta z = z-z_0,$ podemos escribir

\begin{eqnarray}\label{diff02} f'(z_0) = \lim_{\Delta z \rightarrow 0} \frac{f(z_0+\Delta z)-f(z_0)}{\Delta z}. \end{eqnarray}

Usualmente omitimos el sub-índice en $z_0$ e introducimos el número \[\Delta w = f(z+\Delta z)-f(z).\] el cual denota el cambio en el valor $w=f(z)$ correspondiente al cambio $\Delta z$ en el punto en el cual $f$ está evaluada. Entonces podemos escribir la ecuación (\ref{diff02}) como \[\frac{d w}{d z}= \lim_{\Delta z \rightarrow 0}\frac{\Delta w}{\Delta z}.\]

A pesar del hecho de que la fórmula (\ref{diff01}) para una derivada es idéntica en forma a la derivada de una función real, debemos notar que $f'(z_0)$ se trata de un límite de dos dimensiones. De esta forma para que $f'(z_0),$ el límite relevante debe existir independientemente de la dirección en la cual $z$ se aproxima al punto límite $z_0.$ Para una función de una variable real sólo tenemos dos direcciones, esto es, $x\lt x_0$ y $x\gt x_0.$

Existe una variedad infinita de direcciones para aproximarse a $z_0.$

Una característica importante de la diferenciación compleja es que la existencia de una derivada compleja automáticamente implica la existencia de infinitas derivadas. Esto es en contraste con el caso de la función real $g(x),$ en la cual $g'(x)$ puede existir sin la existencia de $g''(x).$

Ecuaciones de Cauchy-Riemann

Para comprender las consecuencias de la definición (\ref{diff01}), veamos qué sucede cuando nos aproximamos a $z_0$ a lo largo de dos direcciones simples - de forma horizontal y vertical. Si definimos $$z= z_0 + h = (x_0+h)+iy_0,\quad h\in \mathbb R,$$ entonces $z \rightarrow z_0$ a lo largo de una línea horizontal cuando $h\rightarrow 0.$ Si escribimos $$f(z) = u(x,y)+iv(x,y)$$ en términos de sus partes real e imaginaria, entonces $$f'(z_0)= \lim_{h \rightarrow 0}\frac{f(z_0+h)-f(z_0)}{h}$$ de lo cual se tenemos que

\begin{eqnarray*} f'(z_0)&= & \lim_{h \rightarrow 0} \frac{f(z_0+h)-f(z_0)}{h} = \lim_{h \rightarrow 0} \frac{f(x_0+h + iy_0)-f(x_0+iy_0)}{h} \\ &= & \lim_{h \rightarrow 0} \left[ \frac{u \left( x_0 +h, y_0 \right) - u \left( x_0 , y_0 \right)}{h}\right]+i \lim_{h \rightarrow 0} \left[ \frac{v \left( x_0 +h, y_0 \right) - v \left( x_0 , y_0 \right)}{h}\right] \\ &= & u_x(x_0, y_0)+ i v_x(x_0,y_0) \end{eqnarray*}

donde $u_x(x_0, y_0)$ y $v_x(x_0,y_0)$ denotan las derivadas parciales de primer orden con respecto a $x$ de las funciones $u$ y $v,$ respectivamente, en $(x_0, y_0).$ Si ahora definimos $$z = z_0+ik = x_0 + i(y_0+k), \quad k\in \mathbb R,$$ entonces $z\rightarrow 0$ a lo largo de la línea vertical cuando $k\rightarrow 0.$ Por lo tanto, también tenemos

\begin{eqnarray*} f'(z_0)&= & \lim_{k \rightarrow 0} \frac{f(z_0+ik)-f(z_0)}{ik} = \lim_{k \rightarrow 0} \left[ -i \frac{f(x_0 + i(y_0+k))-f(x_0+iy_0)}{k} \right] \\ &= & \lim_{k \rightarrow 0} \left[ \frac{v \left( x_0 , y_0 + k\right) - v \left( x_0 , y_0 \right)}{k}-i \frac{u \left( x_0 , y_0 +k \right) - u \left( x_0 , y_0 \right)}{k}\right] \\ &= & v_y(x_0, y_0)- i u_y(x_0,y_0) \end{eqnarray*}

donde las derivadas parciales de $u$ y $v$ son, en este caso, con respecto a $y.$ Cuando igualamos las partes real e imaginaria de estas dos fórmulas para la derivada compleja $f'(z_0),$ descubrimos que las componentes real e imaginaria de $f(z)$ deben satisfacer un sistema lineal homogéneo de ecuaciones diferenciales: $$u_x=v_y, \quad u_y=-v_x.$$ Estas son las ecuaciones de Cauchy-Riemann cuyo nombre se debe a los famosos matemáticos del siglo XIX Augustin-Louis Cauchy y Bernhard Riemann, dos de los fundadores del análisis complejo moderno.

Una función compleja $f(z)=u(x,y)+iv(x,y)$ tiene una derivada compleja $f'(z)$ si y solo si su parte real e imaginaria son diferencialmente continuas y además satisfacen las ecuaciones de Cauchy-Riemann \begin{eqnarray*} u_x=v_y, \quad u_y=-v_x \end{eqnarray*} En este caso, la derivada compleja de $f(z)$ es igual a cualquiera de las siguientes espresiones: $$f'(z)=u_x+iv_x = v_y - i u_y.$$

Ejemplo 1: Considera la función $f(z)=z^2,$ la cual se puede escribir como $$z^2 = \left(x^2-y^2\right)+ i \left(2xy\right).$$ Su parte real $u = x^2-y^2$ e imaginaria $v=2xy$ satisfacen las ecuaciones de Cauchy-Riemann, dado que $$u_x=2x = v_y, \quad u_y = -2y = -v_x.$$ El Teorema 1 implica que $f(z)=z^2$ es diferenciable. Su derivada es

$$f'(z)=u_x+iv_x = v_y - i u_y = 2x + i 2y = 2(x+iy) = 2z.$$

Afortunadamente, la derivada compleja obedece todas las reglas que has aprendido en un curso de cálculo. Por ejemplo

$$\frac{d}{dz}z^n = nz^{n-1}, \quad \frac{d}{dz} e^{cz} = ce^{cz}, \quad \frac{d}{dz} \log z = \frac{1}{z}.$$

Aquí, la potencia $n$ puede ser un número real (o incluso un número complejo debido a la identidad $z^n = e^{n \log z}$), mientras que $c$ es una constante compleja. Las fórmulas exponenciales para las funciones trigonométricas implica que también satisfacen las reglas estándares

\begin{eqnarray*} \frac{d}{dz}\text{sen}\, z &=& \cos z, \quad \frac{d}{dz} \cos z = -\text{sen}\, z.\\ \frac{d}{dz}\text{senh}\, z &=& \cosh z, \quad \frac{d}{dz} \cosh z = \text{senh}\, z. \end{eqnarray*}

Si las derivadas de $f$ y $g$ existen en el punto $z,$ entonces \begin{eqnarray*} \frac{d}{dz}\left[f(z)+g(z) \right]=f^{\prime}(z)+g^{\prime}(z)\\ \frac{d}{dz}\left[f(z)g(z) \right]=f(z)g^{\prime}(z)+f^{\prime}(z)g(z) \end{eqnarray*} y, cuando $g(z)\neq 0,$ \begin{eqnarray*} \frac{d}{dz}\left[\frac{f(z)}{g(z)} \right]=\frac{g(z)f^{\prime}(z)-f(z)g^{\prime}(z)}{\left[g(z)\right]^2} \end{eqnarray*} Finalmente, supongamos que $f$ tiene derivada en $z_0$ y que $g$ tiene derivada en $f (z_0).$ Entonces la función $F(z) = g\left(f (z)\right)$ tiene derivada en $z_0,$ y \begin{eqnarray*} F^{\prime}(z)=g^{\prime}\left(f(z_0)\right)f^{\prime}(z_0) \end{eqnarray*} Nota que las fórmulas para la diferenciación de sumas, productos, razones, inversas y la composición de funciones son idénticas a sus versiones de variable real, con demostraciones similares. De esta forma, afortunadamente, no necesitarás aprender nuevas reglas para realizar el cálculo de derivadas complejas.

Condiciones suficientes para diferenciabilidad

Si se satisfacen las ecuaciones de Cauchy-Riemann en un punto $z_0 = (x_0, y_0),$ esto no es suficiente para asegurar la existencia de la derivada de una función $f(z)$ en ese punto. Sin embargo, al agregar condiciones de continuidad a las derivadas parciales, tenemos el siguiente teorema.

Sea $f(z) = u(x, y) + iv(x, y)$ la función definida en una $\epsilon$ vecindad de un punto $z_0 = x_0 + iy_0,$ y supongamos que (1) las derivadas parciales de primer orden de las funciones $u$ y $v$ con respecto a $x$ y $y$ existen en toda la vecindad; (2) estas derivadas parciales son continuas en $(x_0, y_0)$ y satisfacen las ecuaciones de Cauchy- Riemann $$u_x = v_y,\quad u_y =-v_x$$ at $(x_0, y_0).$ Entonces $f^{\prime}(z_0)$ existe y su valor es $$f^{\prime}(z_0) = u_x + iv_x$$ donde el lado derecho está evaluado en $(x_0, y_0).$

Ejemplo 2: Consideremos la función exponencial $$f (z) = e^z = e^xe^{iy} \quad \quad (z = x + iy),$$ Usando la fórmula de Euler, la podemos re-escribir como $$f(z) = e^x \cos y + ie^x \,\text{sen}\, y,$$ donde $y$ se considera en radianes cuando se evalúan $\cos y$ y $\text{sen}\, y.$ Entonces

$$u(x, y) = e^x \cos y\quad \text{and} \quad v(x, y) = e^x \,\text{sen}\, y.$$

Dado que $u_x = v_y$ y $u_y = -v_x$ se satisfacen y estas derivadas son continuas, las condiciones del teorema se satisface en todos los puntos del plano complejo. De esta manera, $f^{\prime}(z)$ existe, y además

$$f^{\prime}(z) = u_x + iv_x = e^x \cos y + ie^x \,\text{sen}\, y.$$

Nota que $f^{\prime}(z) = f (z)$ para todo $z.$

Una consecuencia de las condiciones en las ecuaciones de Cauchy-Riemann es que las curvas de nivel de $u,$ esto es, las curvas $u(x,y)=c_1$ para $c_1$ una constante real, son ortogonales a las curvas de nivel de $v,$ donde $v(x,y)=c_2,$ en todos los puntos donde $f^{\prime}$ existe y es diferente de cero. Del Teorema 2 tenemos

\begin{eqnarray*} \bigg|f^{\prime}(z)\bigg|^2 &= &\left(\frac{\partial u}{\partial x}\right)^2+\left(\frac{\partial v}{\partial x}\right)^2\\ &=& \left(\frac{\partial u}{\partial x}\right)^2+\left(\frac{\partial u}{\partial y}\right)^2\\ &=& \left(\frac{\partial v}{\partial x}\right)^2+\left(\frac{\partial v}{\partial y}\right)^2 \end{eqnarray*}

por lo que los gradientes en dos dimensiones

\begin{align*} \nabla u &= \left(\frac{\partial u}{\partial x},\frac{\partial u}{\partial y}\right) \quad \text{and}\quad \nabla v = \left(\frac{\partial v}{\partial x},\frac{\partial v}{\partial y}\right) \end{align*}

son diferente de cero. Sabemos del cálculo vectorial que el gradiente es ortogonal a sus curvas de nivel (i. e., $du=\nabla u\cdot \mathbf{ds}=0,$ donde $\mathbf{ds}$ apunta en la dirección de la tangente en la curva de nivel), y de la condición de Cauchy-Riemann del (Teorema 2) podemos observar que los gradientes $\nabla u$ y $\nabla v$ son ortogonales debido que el producto punto es cero:

\begin{eqnarray*} \nabla u\cdot \nabla v&=& \frac{\partial u}{\partial x}\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\frac{\partial v}{\partial y}\\ &=&-\frac{\partial u}{\partial x}\frac{\partial u}{\partial y}+\frac{\partial u}{\partial x}\frac{\partial u}{\partial x}=0 \end{eqnarray*}

Consecuentemente, las curvas de nivel en dos dimensiones $u(x,y)=c_1$ y $v(x,y)=c_2$ son ortogonales.

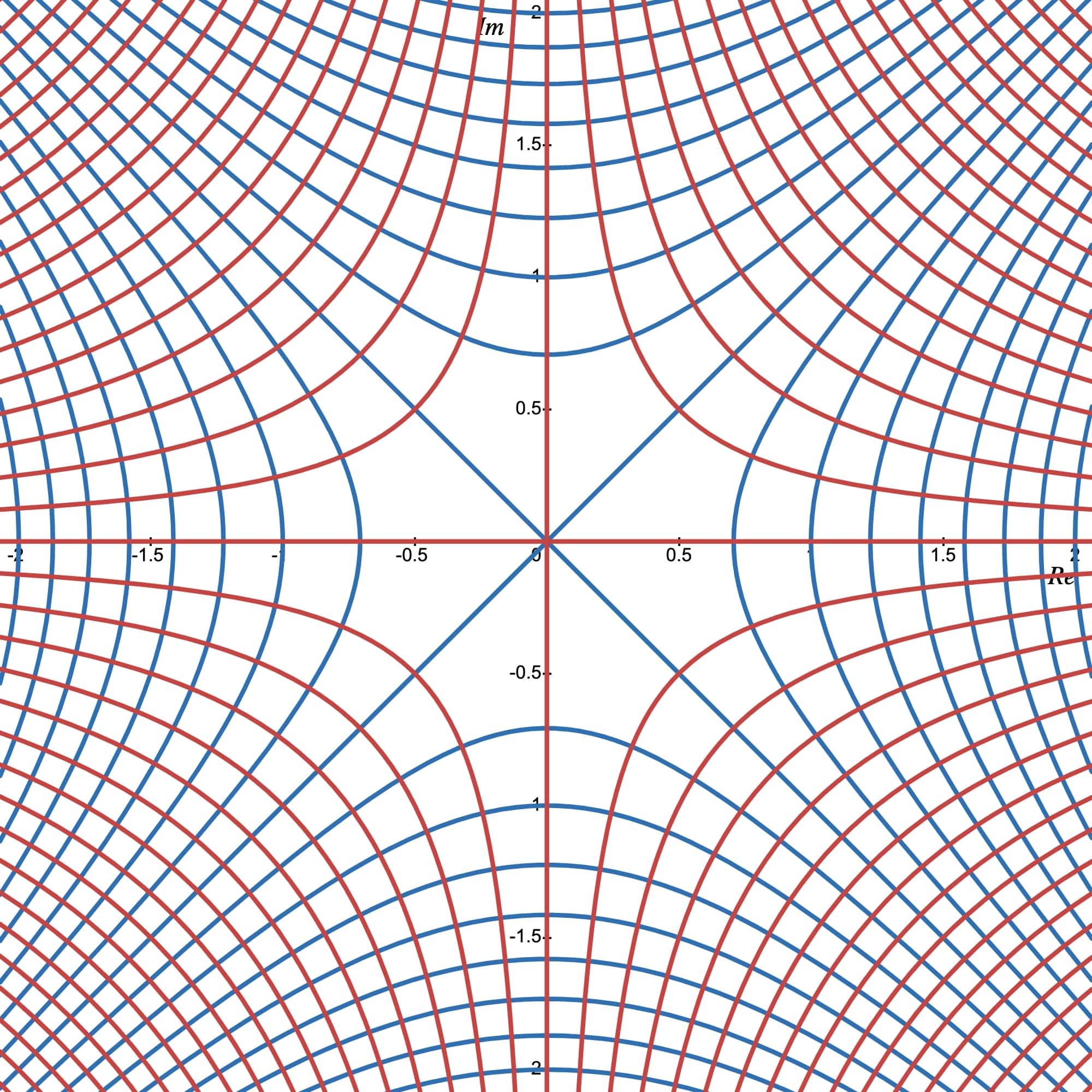
Ejemplo 3: Para la función $f(z) = z^2,$ las curvas de nivel $u(x, y) = c_1$ y $v(x, y) = c_2$ son hipérbolas, como se muestra en la Figura 2. Nota la ortogonalidad de las dos familias de curvas. Observa también que las curvas $u(x, y) = 0$ y $v(x, y) = 0$ se intersectan en el origen pero no son ortogonales la una a la otra.

Orthogonal level curves — Curvas de nivel ortogonales de las componentes real e imaginaria de $f(z) = z^2.$ Gráfica interactiva

Funciones analíticas

Sea $f:A\rightarrow \mathbb C$ donde $A\subset \mathbb C$ es un conjunto abierto. Decimos que la función es analítica en $A$ si $f$ es diferenciable en cada punto $z_0\in A.$ En algunas ocasiones se usa también la palabra "holomórfica", la cual es sinónimo con la "analílica". La frase "analítica en $z_0$" significa que $f$ es analítica en una vecindad de $z_0.$

Una función entera es una función que es analítica en cada punto en todo el plano finito. Dado que la derivada de un polinomio existe en todas partes, se sigue que todo polinomio es una función entera.

Si una función $f$ falla en ser analítica en un punto $z_0$ pero es analítica en alguna vecindad de $z_0,$ entonces $z_0$ se denomina punto singular o singularidad, de $f.$

Ejemplo 4: La función $$f(z) = \frac{1}{z}$$ es analítica en cada punto diferente de cero en el plano finito. Por otra parte, la función $$f(z) = |z|^2$$ no es analítica en cualquier punto ya que su derivada existe solo en $z = 0$ y no sobre una vecidad.

El punto $z = 0$ es evidentemente un punto singular de la función $f(z) = 1/z.$ La función $f(z) = |z|^2,$ por otra parte, no tiene puntos singulares dado que no es analítica en ninguna parte.

Si dos funciones son analíticas en un dominio $D,$ su suma y su producto son ambos analíticos en $D.$ De manera similar, su cociente es analítico en $D$ siempre que la función en el denominador no sea cero en $D.$ En particular, el cociente $$\frac{P(z)}{Q(z)}$$ de dos polinomios es analítico en cualquier dominio en el cual $Q(z)\neq 0.$

Además, de la regla de la cadena para la derivada de una función compuesta, implica que una composición de dos funciones analíticas es analítica.

Ejemplo 5: La función $$f(z) = \frac{4z+1}{z^3-z},$$ es analítica en todo el plano $z$ excepto para los puntos singulares $z=0$ y $z=1,-1.$ La analiticidad de debe a la existencia de las familiares fórmulas de diferenciación, las cuales se necesitan aplicar sólo si se necesita la expresión para $f^{\prime}(z).$ En este caso, tenemos $$f^{\prime}(z)=\frac{-8z^3-3z^2+1}{z^2(z^2-1)^2}.$$

Cuando una función se da en términos de sus componentes $$u(x, y)\quad \text{y}\quad v(x, y),$$ su analiticidad se puede demostrar directamente con la applicación de las ecuaciones de Cauchy-Riemann.

Ejemplo 6: La función $$f(z)=e^ye^{ix}=e^y\cos x +ie^y\,\text{sen}\, x$$ no es analítica en ninguna parte. Sus componentes son $$u(x,y)=e^y\cos x\quad\text{y}\quad v(x,y)=e^y\,\text{sen}\, x.$$ Si $f(z)$ fuera analítica, entonces (usando las ecuaciones de Cauchy-Riemann)

$$u_x=v_y \Rightarrow -e^y\,\text{sen}\, x=e^y\,\text{sen}\, x \Rightarrow 2e^y\,\text{sen}\, x=0 \Rightarrow \text{sen}\, x=0$$

$$u_y=-v_x \Rightarrow e^y\cos x=-e^y\cos x \Rightarrow 2e^y\cos x=0 \Rightarrow \cos x=0.$$

Por otra parte, tenemos que las raíces de $\text{sen}\, x$ son $n\pi$ (with $n\in \mathbb Z$) pero $\cos (n\pi)=(-1)^n\neq0.$ Por otra parte, las raíces de $\cos x$ son $(2n-1)\pi/2$ pero

$$\text{sen}\, ((2n-1)\pi/2)=-\cos(n\pi)=-(-1)^n\neq 0.$$

consecuentemente, las ecuaciones de Cauchy-Riemann no se satisfaces en ninguna parte.

Otra propiedad útil que utilizaremos más adelante es la siguiente:

Si $f'(z) = 0$ en toda una región $D$, entonces $f(z)$ es constante en $D$.

Sean $z_1, z_2 \in D.$ Sea $c(t): [a, b] \to \C$ una curva que conecta $z_1$ con $z_2.$ Es decir, $c(a) = z_1$ y $c(b) = z_2.$ Usando la regla de la cadena, tenemos \[ \frac{d}{dt}f\left(c(t)\right) = f'\left(c(t)\right)\cdot c'(t) = 0, \] ya que $f'(z) = 0$ en todas partes de $D.$ Si $f(z) = u(x,y) + iv(x,y),$ entonces

\[ \frac{d }{dt}u\left(c(t)\right) = 0, \quad \text{y} \quad \frac{d }{dt}v\left(c(t)\right) = 0. \]

Esto implica que $u\left(c(t)\right)$ y $v\left(c(t)\right)$ son funciones constantes de $t.$ Comparando los valores en $t = a$ y $t = b,$ concluimos que $f(z_1) = f(z_2).$ Por lo tanto, $f$ es constante en todo $D.$