Flujo Uniforme Alrededor
de un Círculo

Consideremos un flujo uniforme con velocidad $U,$ dirección con respecto al eje $x,$ con potencial complejo $F(z)=Uz.$ Si agregamos un obstáculo circular impermeable, definido como $|z|=a$ por ejemplo, entonces el flujo se verá afectado como se muestra en la imagen de abajo. El desafío aquí es calcular el flujo perturbado.

Aquí podemos usar el resultado bien conocido en dinámica de fluidos establecido por el matemático L. M. Milne-Thompson:

Supongamos que tenemos un potencial complejo $F(z)$ tal sus singularidades se encuentran en $|z|\gt a.$ Entonces el potencial \begin{eqnarray}\label{circle-theorem} w = F(z) + \overline{F\left(\frac{a^2}{\overline{z}}\right)} \end{eqnarray} (donde la barra denota el conjugado complejo) tiene las mismas singularidades que $F(z)$ en $|z|\gt a$ y el círculo $|z|=a$ es una línea de flujo.

Sea $F(z)$ un potencial complejo tal que todas sus singularidades ocurren solo en la región $|z|\gt a$ (con $a>0$) y define \begin{eqnarray}\label{circle-01} w = F(z) + \overline{F\left(\frac{a^2}{\overline{z}}\right)}. \end{eqnarray} Notemos que si $|z|\gt a,$ entonces $\big|a^2/\,\overline{z}\big|\lt a.$ De esta forma, dado que $F(z)$ no tiene singularidades en $|z|\leq a,$ se sigue que el segundo término de (\ref{circle-01}) tampoco tiene singularidades en $|z|\gt a.$ Esto significa que $F$ y $w$ tienen singularidades en $|z|\gt a.$

Ahora estamos interesados en conocer lo que sucede en la frontera circular $|z|=a.$ En este caso tenemos que $\overline{z} \cdot z = a^2.$ Es decir $$z= \frac{a^2}{\overline{z} }.$$ De esta manera, $$\big. w \big|_{|z|=a}= F(z)+ \overline{F\left(\frac{a^2}{\overline{z}}\right)} = F(z) + \overline{F\left(z\right)} = 2 \text{Re}\left(f(z)\right),$$ la cual es completamente real. Por lo tanto en la frontera $|z|=a$ $$\psi = \text{Im}\, w = 0.$$ Esto demuestra que el círculo $|z|=a$ es una línea de flujo.

Notemos que el potencial complejo $F(z)=Uz$ satisface la hipótesis del Teorema del Círculo. Entonces podemos obtener el potencial complejo del flujo uniforme alrededor del círculo al sustituir $F(z)=Uz$ en la ecuación (\ref{circle-theorem}): \begin{eqnarray}\label{potential} w = Uz + \overline{\frac{Ua^2}{\overline{z}}} = Uz + \frac{Ua^2}{z}. \end{eqnarray}

Consecuentemente, la función de flujo es justamente la componente imaginaria de (\ref{potential}), es decir \begin{eqnarray*} \psi = Uy\left(1- \frac{a^2}{x^2+y^2} \right). \end{eqnarray*} y podemos observar que el círculo $x^2+y^2=a^2$ es de hecho una línea de flujo, con $\psi=0.$ El flujo resultante se muestra en la Figura 2 con $a=1.$

Uniform flow — Flujo uniforme alrededor de un círculo.

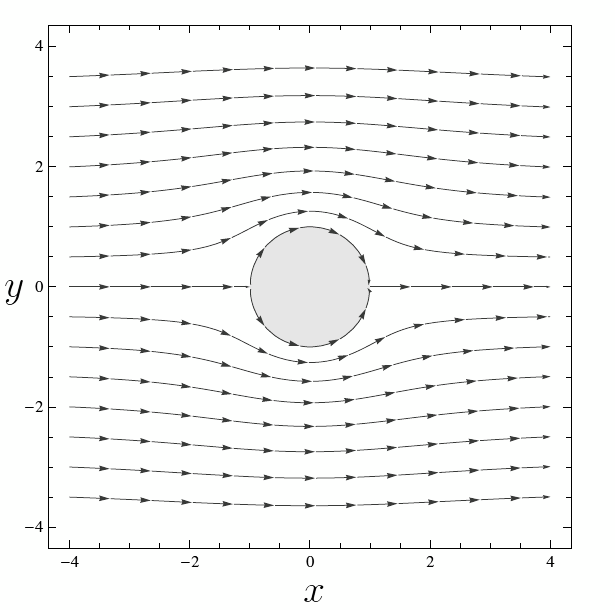
Es probable que hayas notado que (\ref{potential}) tiene una singularidad en $z=0.$ Este tipo de singularidad se conoce como un doblete y corresponde a la función $Ua^2/z.$ La singularidad en el origen está en el interior del obstáculo y de esta manera no afecta el flujo externo. El patrón de las líneas de flujo, incluyendo el doblete dentro del círculo, se muestra en la Figura 3.

Doublet — Líneas de flujo causadas por un doblete en un flujo uniforme.

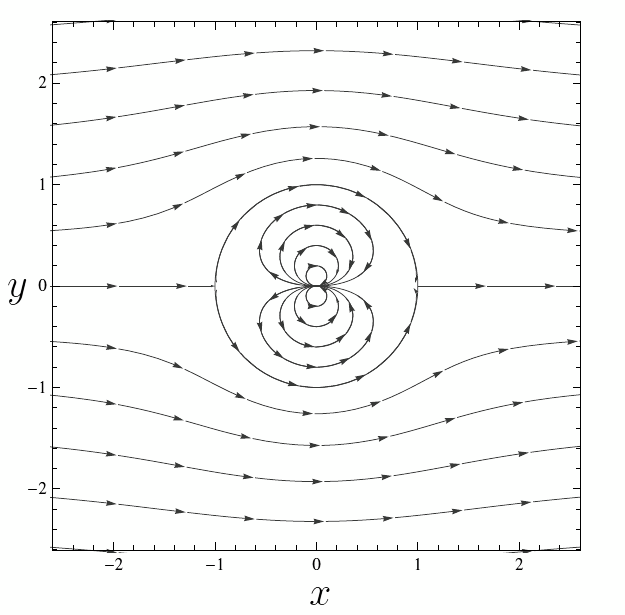
Ejercicio: Demuestra que las componentes del vector velocidad $\mathbf V = (u, v)$ para el flujo uniforme alrededor del círculo están definidas como

\begin{eqnarray*} u = U\left(1 - a^2\frac{x^2-y^2}{\left(x^2+y^2\right)^2}\right),\quad v= -2 U^{2} a^{2} \frac{ x y}{ \left(x^{2} + y^{2} \right)^{2}} \end{eqnarray*}

donde $U$ es la velocidad y $a$ es el radio.

Flujo uniforme alrededor el círculo con circulación

Si agregamos un vórtice al potencial complejo definido en (\ref{potential}), obtenemos un flujo uniforme alrededor un círculo con circulación: \begin{eqnarray}\label{circulation} w = Uz + \frac{Ua^2}{z} - \frac{iC}{2\pi}\log z, \end{eqnarray} donde $C\in \mathbb R$ representa la circulación alrededor del círculo.

En este caso, la función de flujo es

\begin{eqnarray*} \psi = U y \left( 1 - \frac{a^2}{x^2+y^2} \right) - \frac{C}{4\pi} \log\left(x^2+y^2\right). \end{eqnarray*}

Notemos que el círculo $x^2+y^2=a^2$ todavía sigue siendo una línea de flujo, con $\psi = - (C/2\pi)\log a.$ Cualquier punto de estancamiento en el flujo satisface la ecuación $$0 = U - \frac{Ua^2}{z^2} - \frac{iC}{2\pi z},$$ la cual se puede re-escribir como la ecuación cuadrática $$z^2-2i\gamma a z - a^2 = 0, \quad \text{with}\quad \gamma =\frac{C}{4\pi Ua}.$$ Las raíces de esta ecuación son $$\frac{z}{a} = i\gamma \pm \sqrt{1-\gamma^2}.$$

De esta manera cuando $\gamma = 0,$ no hay circulación y los puntos de estancamiento son $z =\pm a.$ Cuando $\gamma$ incrementa, la circulación será anti horaria causa que los puntos de estancamiento se mueven hacia arriba alrededor del círculo. Cuando toma el valor de 1, los dos puntos de estancamiento coinciden en la parte superior del cilindro $z = ia.$ Si $\gamma > 1,$ entonces un punto de estancamiento se mueve hacia el flujo; mientras que el otro punto se encuentra dentro del círculo.

Explora todos los casos en el applet a continuación, el cual muestra el flujo y un círculo de radio 1. Arrastra los controles deslizantes $ U $ y $ C $ para cambiar la velocidad y la circulación, respectivamente.

Ejercicio: Demuestra que las componentes del vector velocidad $\mathbf V = (u, v)$ para el flujo uniforme alrededor de un círculo con circulación están dadas por

\begin{eqnarray*} u &=& U\left(1 - a^2\frac{x^2-y^2}{\left(x^2+y^2\right)^2}\right) - \frac{C}{2\pi}\frac{y}{x^2+y^2},\\ v &=& -2 U^{2} a^{2} \frac{ x y}{ \left(x^{2} + y^{2} \right)^{2}} + \frac{C}{2\pi}\frac{x}{x^2+y^2} \end{eqnarray*}

donde $U$ es la velocidad, $a$ es el radio y $C$ es la circulación.

Flujo Uniforme Alrededor de un Círculo

Flujo uniforme alrededor el círculo con circulación

Flujo Uniforme Alrededor
de un Círculo