Cauchy-Goursat Theorem

Cauchy's Theorem

In 1825 the French mathematician Augustin-Louis Cauchy proved one of the most important theorems in complex analysis:

If the function is not analytic on the whole region inside $C,$ then the integral may or may not be $0.$ For instance, Let $C$ be the unit circle and $f(z)=1/z.$ Then $f$ is analytic at all points except $z=0,$ and indeed the integral is not zero. In fact, \[ \int_C \frac{1}{z}\,dz = 2\pi i, \] as shown in example 2 from the Complex Integration section. On the other hand, if $f(z) = 1/z^2,$ then $f$ is still analytic at all points except $z=0,$ but now the integral is $0.$ This value results not from Cauchy's Theorem, since $f$ is not analytic everywhere inside $C,$ but rather from the fact that $f$ has an antiderivative on $\C\setminus \{0\}.$ That is, $f$ is the derivative of $F'(z)=-1/z.$

Proof of Theorem 1. The proof of this theorem is an immediate consequence of Green's theorem in the plane, which states that, for continuously differentiable functions $P(x,y)$ and $Q(x,y),$

In Green's theorem, $R$ represents the inside of $C,$ $C$ is traversed in a counterclockwise direction, and $P$ and $Q$ are sufficiently smooth.

Setting $f=u+iv,$ we have

By applying Green's theorem to each integral, we get

Both intergrals, on the right side, are zero by the Cauchy-Riemann equations. $\hspace{5pt} \blacksquare$

Observe that once it has been established that the value of this integral is zero, the orientation of $C$ becomes irrelevant. The conclusion in Theorem 1 is also true if $C$ is taken in the clockwise direction, since then we can use the fact that \[ \int_C f(z)\,dz = - \int_{-C} f(z)\,dz. \]

Cauchy-Goursat Theorem

In 1900 the French mathematician Edouard Goursat proved that the assumption of continuity of $f'$ is not necessary to reach the conclusion of Cauchy's theorem. The resulting modified version of Cauchy's theorem is known today as the Cauchy-Goursat Theorem. as we can expect, with fewer hypotheses, the proof of this version of Cauchy's theorem is more complicated than the one just presented.

Simply and multiply connected domains

We say that a domain $D$ is simply connected if every simple closed contour $C$ lying entirely in $D$ can be shrunk to a point without leaving $D.$ See Figure 3. In other words, if we draw any simple closed contour $C$ so that it lies entirely within a simply connected domain, then $C$ encloses only points of the domain $D.$

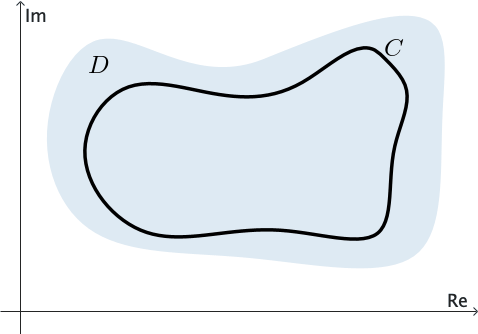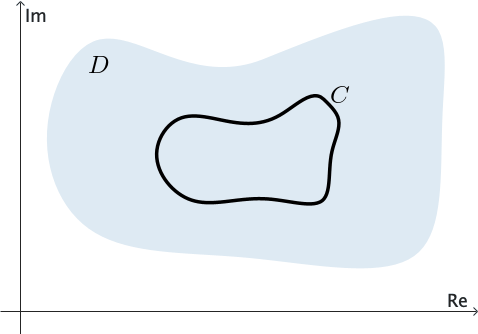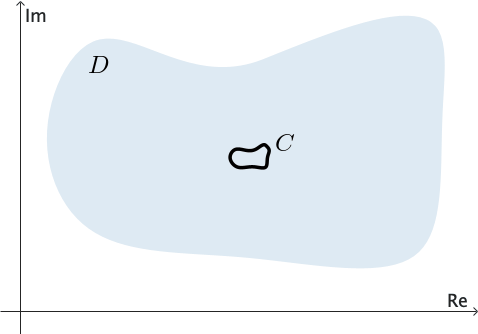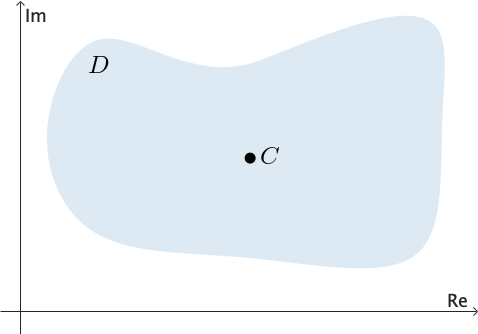
In other words, a simply connected domain has no "holes" in it. The entire complex plane is an example of a simply connected domain; the annulus defined by $1 \lt |z| \lt 2$ is not simply connected.

A domain that is not simply connected is called a multiply connected domain; that is, a multiply connected domain has "holes" in it. For example, note in Figure 5 that if the curve $C$ enclosing the "hole" (on the left side) is shrunk to a point, the curve would have to leave $D$ eventually.

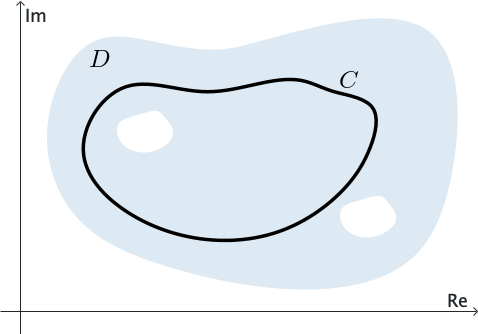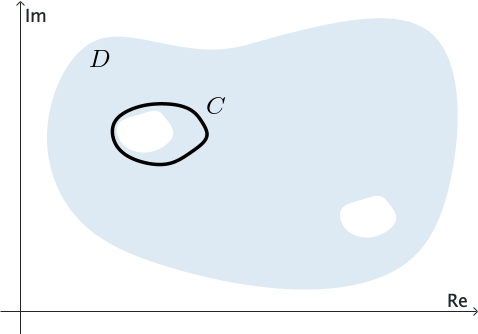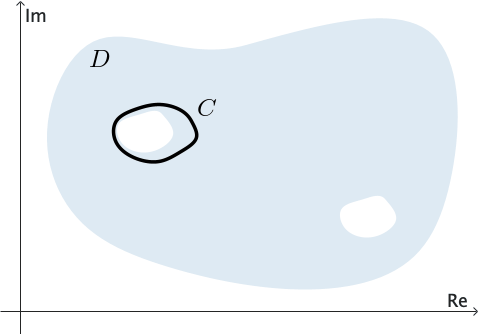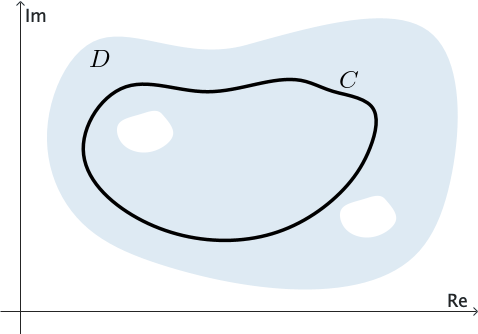
The closed contour in the Cauchy-Goursat Theorem does not need to be simple when the theorem is adapted to simply connected domains. That is, the contour can actually cross itself. The following theorem allows for this possibility.

The proof is easy if $C$ is a simple closed contour or if it is a closed contour that intersects itself a finite number of times. In the case that $C$ is simple and lies in $D,$ the function $f$ is analytic at each point interior to and on $C.$ The Cauchy-Goursat Theorem ensures that the conclusion of Theorem 3 holds. On the other hand, if $C$ is closed but intersects itself a finite number of times, it consists of a finite number of simple closed contours. This is illustrated in Figure 6, where the simple closed contours $C_k$ $(k = 1, 2, 3, 4)$ make up $C.$ Since the value of the integral around each $C_k$ is zero, according to the Cauchy-Goursat theorem, it follows that

Example 4: Let $C$ be any closed contour lying in the open disk $|z|\lt 2.$ Then \[ \int_C \frac{z\sin(z)}{\left(z^2-9\right)^3}dz =0. \] Note that the disk is a simply connected domain and the two singularities $z=\pm 3$ of the integrand are outside the disk.

If $f$ is analytic in a multiply connected domain $D$ then we cannot conclude that $\int_C f(z)\,dz=0$ for every simple closed contour $C$ in $D.$ Suppose that $D$ is muliply connected with two "holes". Let $C,$ $C_1$ and $C_2$ be simple closed contours such that each $C_k$ surrounds only one "hole" in the domain and are inside $C.$ See Figure 8.

Now, suppose also that $f$ is analytic on each contour and throughout the multiply connected domain consisting of the points inside $C$ and exterior to each $C_k.$ Assume that $C$ is described in the counterclockwise direction and each $C_k$ is described in the clockwise direction. We introduce a polygonal path $L_1,$ consisting of a finite number of line segments joined end to end, to connect the outer contour $C$ to the inner contour $C_1.$ As shown in Figure 9, we introduce another polygonal path $L_2$ which connects $C_1$ to $C_2;$ and finally another polygonal path $L_3$ connecting $C_3$ to $C.$

As indicated in Figure 10, two simple closed contours $\Gamma_1$ and $\Gamma_2$ can be formed, each consisting of polygonal paths $L_k$ or $-L_k$ and pieces of $C$ and $C_k$ and each described in such a direction that the points enclosed by them lie to the left. Here we can apply the Cauchy-Goursat Theorem to $f$ on $\Gamma_1$ and $\Gamma_2,$ and the sum of the values of the integrals over those contours is found to be zero. Since the integrals in opposite directions along each path $L_k$ cancel, only the integrals along $C$ and the $C_k$ remain. Thus we obtain

The next theorem summarizes the general result for a multiply connected domain with $n$ “holes.”

The following corollary is known as the principle of deformation of contours since it tells us that if $C_1$ is continuously deformed into $C_2$ always passing through points at which $f$ is analytic, then the value of the integral of $f$ over $C_1$ never changes.

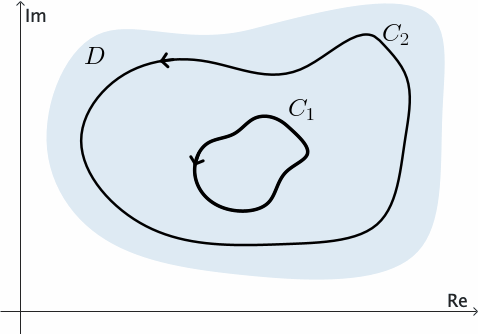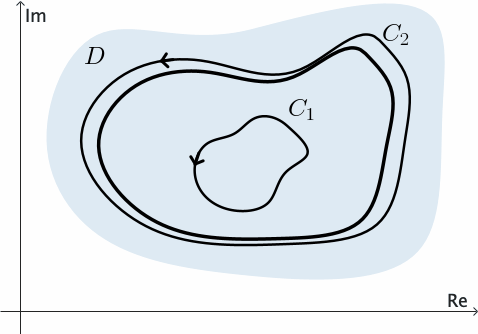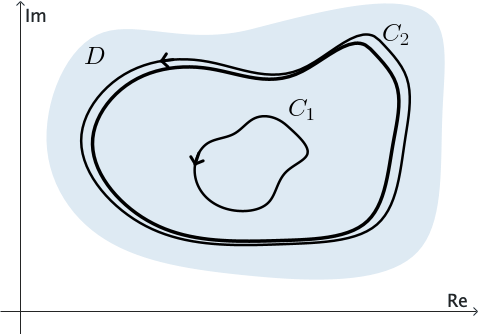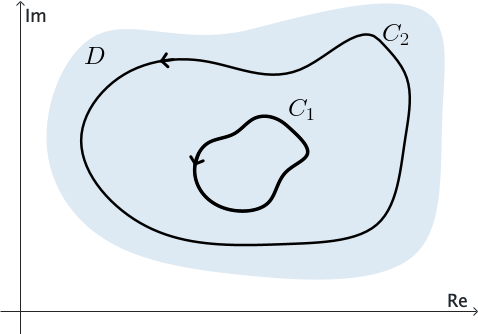
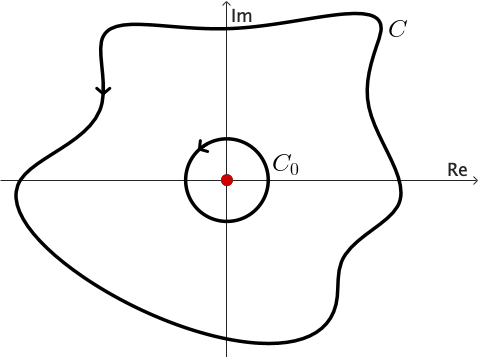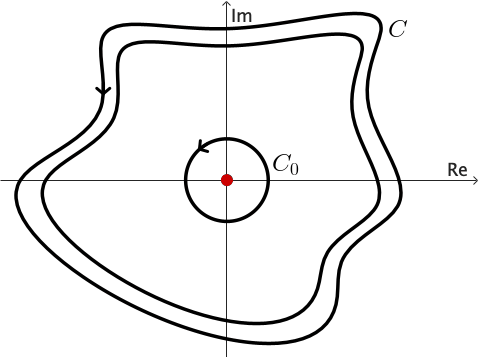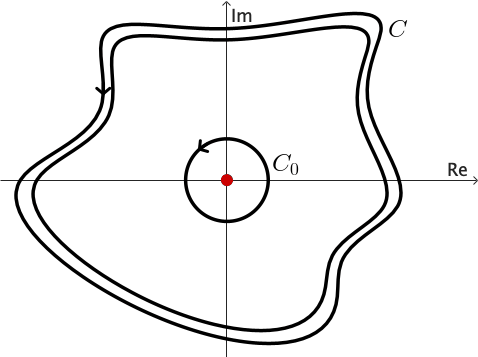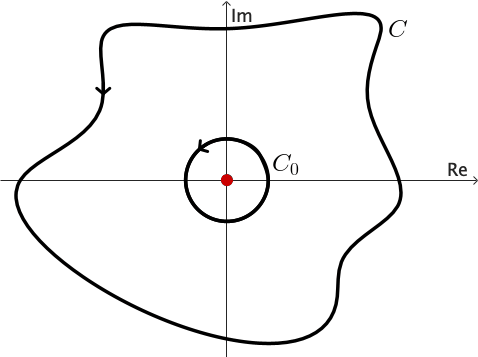
Example 5: We can use the previous corollary to show that \[ \int_C \frac{1}{z} dz= 2\pi \,i \] for any positively oriented simple closed contour $C$ surrounding the origin.

Consider $C_0$ a positively oriented circle with center at the origin and radius so small that $C_0$ lies entirely inside $C.$

We know that (see example 2 from the Complex Integration section) \[ \int_{C_0} \frac{1}{z} dz= 2\pi \,i. \] and since $1/z$ is analytic everywhere except at $z = 0,$ the result follows easily.

Historical notes & Proof

Cauchy first communicated the integral theorem to the Académie des Sciences in 1814, as part of a memoir related with other topics (improper real integrals) [1 pp. 132-133, 4, 13 pp. 56-57]. The first general form of the integral theorem was communicated to the Académie in 1825 in a memoir entitled Mémoire sur les intégrales définies, prises entre des limites imaginaires [1 pp. 151-156, 5, 13 pp. 89-91].

Goursat presented a proof Cauchy's Theorem in 1884 for the case of a simple closed curve, by dividing up the interior into small squares, showing that the integral around each square of side $\ell$ is bounded by $\epsilon \ell ^2,$ and then adding the results. To obtain this estimate for arbitrary $\epsilon$ he needs the uniform continuity of $f'$ [7]. In his 1900 paper, Goursat finally removed the assumption of continuity of $f'$ [2, 8]. The argument is as before, but he now subdivides each square until the necessary estimate holds for each of them, that is,

for every $z$ on the boundary of the subsquare, where $z_0$ is some fixed point in the subsquare. The important point here is that the same $\epsilon$ will do for each subsquare.

In 1900, Eliakim H. Moore refined the proof, addressing the treatment of the boundary curve with greater precision [11]. He also introduced the modern approach of proof by contradiction, which involves subdividing the domain, selecting the region where the conclusion is most significantly contradicted, and then applying the definition of the derivative at the resulting limit point [9, p. 651].

Later in 1901 Alfred Pringsheim presented a criticism of Goursat's treatment of the boundary curve [12]. He observed that these issues vanish when the proof technique is applied to a basic geometric shape, such as a triangle. From there, the theorem extends to simple polygonal paths within a simply connected domain by triangulating the interior of the path. Finally, it can be generalized to arbitrary paths by approximating them with polygonal paths. [9, p. 651]. This is the method that we will use to prove the Cauchy-Goursat Theorem.

To avoid needless repetition throughout the following discussion we will take for granted that we are working in a simply connected domain $D$ and that $f$ represents a complex function analytic in $D.$

Let $\Delta$ be the triangular contour shown in Figure 13. The vertices of $\Delta$ are labeled $V_1,V_2$ and $V_3.$ We form smaller triangles $\Delta_1, \Delta_2,$ $\Delta_3$ and $\Delta_4$ by joining the midpoints $M_1,M_2$ and $M_3$ of the sides of $\Delta$ by straight line segments as shown in Figure 14. Then

\begin{eqnarray}\label{sumcontours} \int_{\Delta} f(z)\,dz = \int_{C_1} f(z)\,dz +\int_{C_2} f(z)\,dz +\int_{C_3} f(z)\,dz +\int_{C_4} f(z)\,dz. \end{eqnarray}

Using the triangle inequality we have

\begin{eqnarray}\label{triangle01} \left|\int_{\Delta} f(z)\,dz\right| \leq \left|\int_{C_1} f(z)\,dz\right| + \left|\int_{C_2} f(z)\,dz\right| + \left|\int_{C_3} f(z)\,dz\right| + \left|\int_{C_4} f(z)\,dz\right|. \end{eqnarray}

Since the four quantities on the right side of the previous inequality are nonnegative real numbers and, as a consequence, one of them must be greater than or equal to the other three. Let's denote the triangular contour of the integral with the largest modulus by the symbol $\Delta_1.$ Thus \begin{eqnarray}\label{triangle02} \left|\int_{\Delta} f(z)\,dz\right| \leq 4 \left|\int_{\Delta_1} f(z)\,dz\right| . \end{eqnarray}

Now we repeat the foregoing process for the triangle $\Delta_1.$ That is, we form triangles within $\Delta_1$ by joining the midpoints of its sides by line segments in the same way as shown in Figure 14 and proceed to the equivalent of (\ref{sumcontours}) and (\ref{triangle01}). The integral of $f$ along one of these new triangular contous, let's call it $\Delta_2$ then satisifies \[ \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4 \left|\int_{\Delta_2} f(z)\,dz\right| . \]

We combine this last inequality with (\ref{triangle02}) to obtain \[ \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4 \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4^2 \left|\int_{\Delta_2} f(z)\,dz\right| . \]

We continue in this way to obtain a sequence of "nested" triangular contours $\Delta, \Delta_1, \Delta_2,\ldots,$ that is, each triangle in the sequence is contained in the one immediately preceding it. After $n$ steps we get \begin{eqnarray}\label{bound4} \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4^n \left|\int_{\Delta_n} f(z)\,dz\right| . \end{eqnarray}

Since the sequence triangular contours $\Delta, \Delta_1, \Delta_2,\ldots,$ are nested, there exists a point $z_0$ in the domain $D$ that is common to every triangle in the sequence. Also, since $f$ is analytic, then $f'(z_0)$ exists. If we define \begin{eqnarray}\label{lambda} \Lambda(z) = \frac{f(z)-f(z_0)}{z-z_0} - f'(z_0), \end{eqnarray} then $\left|\Lambda(z)\right|$ can be made arbitrarily small whenever $z$ is sufficiently close to $z_0.$ This is true because $f$ is analytic in $D$ and so the limit \begin{eqnarray*} \lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0} \end{eqnarray*} exists and is equal to $f'(z_0).$ In other words, for every $\epsilon\gt 0,$ there exist $\delta\gt 0$ such that

\begin{eqnarray}\label{smallenough} \left|\Lambda(z)\right|\lt \epsilon \quad \text{whenever}\quad \left|z-z_0\right|\lt \delta. \end{eqnarray}

We can solve (\ref{lambda}) for $f(z)$ and replace this value in the integrand in (\ref{bound4}) to obtain

\begin{eqnarray}\label{expanded} \int_{\Delta_n}f(z)\,dz = f(z_0) \int_{\Delta_n}dz + f'(z_0)\int_{\Delta_n}(z-z_0)\,dz + \int_{\Delta_n}(z-z_0)\Lambda(z)\,dz. \end{eqnarray}

Since \[ \int_{\Delta_n}dz =0 \quad \text{and}\quad \int_{\Delta_n}(z-z_0)\,dz=0 \] (Why?), the right side of (\ref{expanded}) reduces to \begin{eqnarray}\label{reduced} \int_{\Delta_n}f(z)\,dz = \int_{\Delta_n}(z-z_0)\Lambda(z)\,dz. \end{eqnarray}

Now let $L$ and $L_1$ denote the lengths of the triangular contours $\Delta$ and $\Delta_1,$ respectively. Then, if we keep in mind how the triangle $\Delta_1$ was constructed, it is a straightforward problem in similar triangles to show that $L_1$ is related to $L$ by $L_1=\dfrac{1}{2}L.$ Likewise, if $L_2$ is the legth of $\Delta_2,$ then $L_2=\dfrac{1}{2}L_1 = \dfrac{1}{2^2}L.$ In general we have that if $L_n$ is the length of $\Delta_n,$ then $L_n= \dfrac{1}{2^n}L.$

For any $z\in \Delta_n,$ we have that $\abs{z-z_0}\lt L_n,$ where $\ds L_n= \frac{1}{2^n}L.$ If we choose $n$ large enough so that \[ \abs{z-z_0}\lt \frac{1}{2^n}L\lt \delta, \] it then follows from (\ref{reduced}), (\ref{smallenough}) and the ML-inequality

\begin{eqnarray}\label{boundgeneral} \abs{\int_{\Delta_n}f(z)\,dz } = \abs{ \int_{\Delta_n}(z-z_0)\Lambda(z)\,dz} \leq \frac{L}{2^n}\cdot \epsilon \cdot \frac{L}{2^n} = \frac{L^2}{4^n}\epsilon \end{eqnarray}

Putting (\ref{bound4}) together with (\ref{boundgeneral}) gives us a bound for the modulus of the integral on $\Delta:$ \begin{eqnarray}\label{lastbound} \abs{\int_{\Delta}f(z)\,dz } \leq 4^n \frac{L^2}{4^n}\epsilon = L^2\epsilon. \end{eqnarray} Since $\epsilon \gt 0$ can be made arbitrarily small, then $\abs{\int_{\Delta}f(z)\,dz}=0.$ Therefore \begin{eqnarray*} \int_{\Delta}f(z)\,dz =0. \end{eqnarray*}

Exercise 2: Use Lemma 1 and the fact that any closed polygonal contour $C$ can be "triangulated" to prove Lemma 2.

Remark: Roughly, "triangulated" means that the closed polygon $C$ can be decomposed into a finite number of triangles by adding lines as shown in Figure 16. Note that we can then proceed as in the proof of Lemma 1 and integrate twice along these added line segments but in opposite directions. If the closed polygon $C$ has $n$ sides, then it can be decomposed into n triangles $C_1,C_2, \ldots, C_n$ and we would eventually arrive at the following analogue of (\ref{sumcontours}): \[ \int_C f(z)\,dz = \sum_{k=1}^{n} \int_{C_k}f(z)\,dz. \]

Now the Cauchy-Goursat Theorem can easily be proved using Lemma 2 and the fact that any closed contour $C$ can be approximated to any desired degree of accuracy by a closed polygonal path.

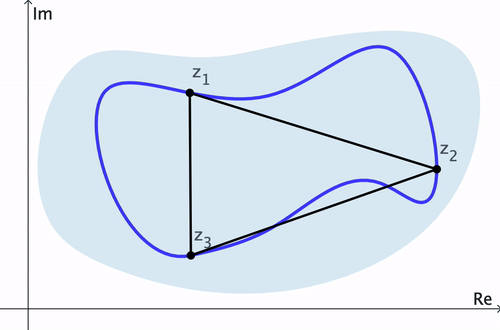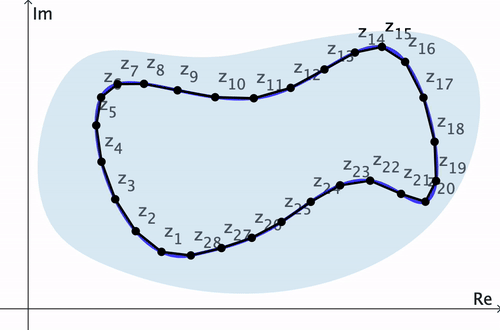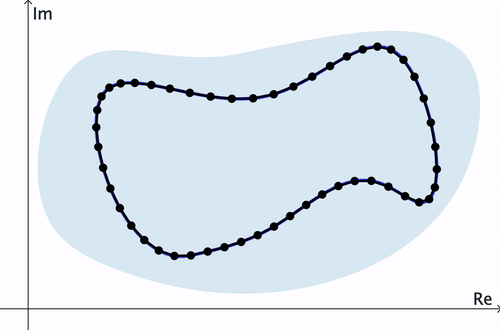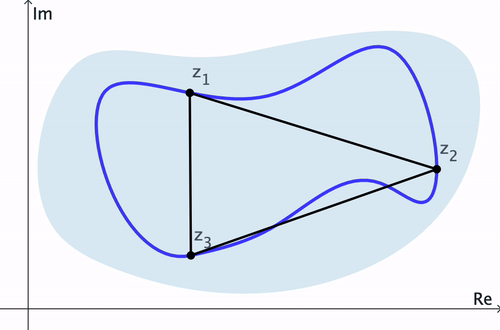
Proof of Cauchy-Goursat Theorem. Consider a simple closed contour $C$ and $n$ points $z_1, z_2, \ldots, z_n$ on $C$ through wich a polygonal path $P$ has been constructed. Then it can be shown that the difference \[ \abs{\int_C f(z)\,dz - \int_P f(z)\,dz} \] can be made arbitrarily small as $n\to \infty.$ Thus, by Lemma 2, $\ds \int_P f(z)\,dz = 0$ for any $n.$ Therefore $\ds \int_C f(z)\,dz=0.$ $\hspace{10pt}\blacksquare$

The Cauchy-Goursat Theorem has been established through various methods. For instance, proofs have been constructed specifically for rectangles or disks (see [3, 10]). Beyond these approaches, many other proofs of the theorem have been developed. Notably, John D. Dixon presented a concise and elegant proof relying only on fundamental concepts of complex function theory in convex sets [6]. Rudolf Výborný, on the other hand, offered a proof based on differentiable homotopy [14].

References

1. Bottazzini, U. (1984). The higher calculus: a history of real and complex analysis from Euler to Weierstrass. New York : Springer-Verlag.
2. Borger, R. L. (1921). On the Cauchy-Goursat theorem, Bulletin of the American Mathematical Society, Vol. 27, No. 7, pp. 325-329.
3. Brown, J. W., Churchill, R. V. (2009). Complex Variables and Applications. 8th Edition. New York: McGraw-Hill Higher Education.
4. Cauchy, A. (1814). Mémoire sur la théorie des intégrales définies, in Œuvres complètes d'Augustin Cauchy, $\text{I}^{re}$ série, vol. I, Gauthier Villars, Paris.
5. Cauchy, A. (1825). Mémoire sur les intégrales définies, prises entre des limites imaginaires, in Œuvres complètes d'Augustin Cauchy, $\text{II}^{e}$ série, vol. XV, Gauthier Villars, Paris.
6. Dixon, J. D. (1971). A brief proof of Cauchy's integral theorem, Proceedings of the American Mathematical Society, Vol. 29, No. 3, pp. 625-626.
7. Goursat, E. (1884). Démonstration du théorème de Cauchy. Acta Mathematica, 4, pp. 197-200.
8. Goursat, E. (1900). Sur la définition générale des fonctions analytiques, d'après Cauchy, Transactions of the American Mathematical Society, Vol. 1, No. 1, pp. 14-16.
9. Hance-Olsen, H. (2008). On Goursat's Proof of Cauchy's Integral Theorem, The American Mathematical Monthly, 115, pp. 648-652.
10. Marsden, J. E. & Hoffman, M. J. (1999) Basic Complex Analysis. (3rd ed.) New York: W. H. Freeman and Co.
11. Moore, E. H. (1900). A Simple Proof of the Fundamental Cauchy-Goursat Theorem, Transactions of the American Mathematical Society, Vol. 1, No. 4, pp. 499-506.
12. Pringsheim, A. (1901). Ueber den Goursat'schen Beweis des Cauchy'schen Integralsatzes, Transactions of the American Mathematical Society, Vol. 2, No. 4, pp. 413-421.
13. Smithies, F. (1997). Cauchy and the Creation of Complex Function Theory. UK: Cambridge University Press.
14. Výborný, R. (1979). On the Use of a Differentiable Homotopy in the Proof of the Cauchy Theorem, The American Mathematical Monthly, Vol. 86, No. 5, pp. 380-382.