Teorema de Cauchy-Goursat

Teorema de Cauchy

En 1825, el matemático francés Augustin-Louis Cauchy demostró uno de los teoremas más importantes en el análisis complejo:

(Teorema de Cauchy) Supongamos que $f$ es analítica, con la derivada $f'$ continua sobre y dentro de un contorno simple cerrado $C.$ Entonces \[ \int_C f(z)\, dz = 0. \]

Cauchy's Theorem — El Teorema de Cauchy implica que $\displaystyle \int_C f(z)\,dz =0.$

Si la función no es analítica en toda la región dentro de $C,$ entonces la integral puede o no ser igual a $0.$ Por ejemplo, sea $C$ el círculo unitario y $f(z)=1/z.$ Entonces $f$ es analítica en todos los puntos excepto en $z=0,$ y, de hecho, la integral no es cero. En efecto, \[ \int_C \frac{1}{z}\,dz = 2\pi i, \] como se muestra en el ejemplo 2 de la sección Integración Compleja. Por otro lado, si $f(z) = 1/z^2,$ entonces $f$ sigue siendo analítica en todos los puntos excepto en $z=0,$ pero ahora la integral es $0.$ Este valor no resulta de manera directa del Teorema de Cauchy, ya que $f$ no es analítica en toda la región dentro de $C,$ sino más bien del hecho de que $f$ tiene una antiderivada en $\C\setminus \{0\}.$ Es decir, $f$ es la derivada de $F'(z)=-1/z.$

Demostración del Teorema 1. La demostración de este teorema es una consecuencia inmediata del Teorema de Green en el plano, el cual establece que, para funciones $P(x,y)$ y $Q(x,y)$ continuamente diferenciables,

\begin{eqnarray}\label{green-theo} \int_C P\,dx + Q\, dy & =& \iint_R \left(\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}\right) dA \end{eqnarray}

En el teorema de Green, $R$ representa el interior de $C,$ $C$ se recorre en sentido antihorario, y $P$ y $Q$ son funciones suficientemente suaves.

Al establecer $f=u+iv,$ tenemos

\begin{eqnarray*} \int_C f(z)\,dz & =& \int_C \left(u+iv\right) \left(dx+idy\right)\\ & =& \int_C \left(u\,dx - v\,dy \right) + i \int_C \left(u\, dy+v \,dx\right). \end{eqnarray*}

Aplicando el teorema de Green a cada integral, obtenemos

\begin{eqnarray*} \int_C f(z)\,dz & =& \iint_R \left(-\frac{\partial v}{\partial x} - \frac{\partial u}{\partial y}\right) dA + i \iint_R \left(\frac{\partial u}{\partial x} - \frac{\partial v}{\partial y}\right) dA \\ \end{eqnarray*}

Ambas integrales en el lado derecho son cero debido a las ecuaciones de Cauchy-Riemann. $\hspace{5pt} \blacksquare$

Observemos que, una vez establecido que el valor de esta integral es cero, la orientación de $C$ se vuelve irrelevante. La conclusión del Teorema 1 también es válida si $C$ se toma en sentido horario, ya que podemos usar el hecho de que \[ \int_C f(z)\,dz = - \int_{-C} f(z)\,dz. \]

Ejemplo 1: Considera la función $f(z)= \exp\left(z^3\right).$ Si $C$ es cualquier contorno cerrado simple, en cualquier dirección, entonces \[ \int_C \exp\left(z^3\right)\,dz =0. \] En este caso, $f$ es la composición de dos funciones, ambas analíticas en todo punto. Por lo tanto, $f$ también es analítica, y su derivada $f'(z) = 3z^2\exp\left(z^3\right)$ es continua en todo punto.

Teorema de Cauchy-Goursat

En 1900, el matemático francés Edouard Goursat demostró que la suposición de continuidad de $f'$ no es necesaria para llegar a la conclusión del teorema de Cauchy. La versión modificada resultante del teorema de Cauchy se conoce hoy en día como el Teorema de Cauchy-Goursat. Como era de esperarse, con menos hipótesis, la demostración de esta versión del teorema de Cauchy es más complicada que la que acabamos de presentar.

(Teorema de Cauchy-Goursat) Si una función $f$ es analítica en todos los puntos interiores a un contorno cerrado simple $C$ y en el propio contorno, entonces \[ \int_C f(z) \, dz = 0. \]

Ejemplo 2: La función $f(z)=\exp(z)$ es entera y, en consecuencia, es analítica en todos los puntos dentro y sobre cualquier contorno cerrado simple $C.$ Se deduce del Teorema de Cauchy-Goursat que \[ \int_C \exp(z)\,dz = 0. \] De manera similar, dado que $\sin z,$ $\cos z$ y

\begin{eqnarray*} p(z) = a_nz^n+ a_{n-1}z^{n-1} + \cdots + a_1 z + a_0, \quad (n =0,1,2,\ldots) \end{eqnarray*}

son funciones enteras, entonces

\begin{eqnarray*} \int_C \sin z\,dz = 0,\quad \int_C \cos z\,dz = 0,\quad \int_C p(z)\,dz = 0. \end{eqnarray*}

para cualquier contorno cerrado simple $C$.

Ejemplo 3: Podemos usar el Teorema de Cauchy-Goursat para evaluar \[ \int_C \frac{1}{z^2}\,dz, \] donde $C$ es la elipse $(x-2)^2+\dfrac{1}{4}(y-5)^2=1.$ Observa que la función $f(z)=1/z^2$ es analítica en todos los puntos excepto en $z=0.$ En este caso, $z=0$ no está dentro ni sobre el contorno elíptico cerrado simple $C.$ Por lo tanto, \[ \int_C \frac{1}{z^2}\,dz=0. \]

El contorno elíptico $C.$ Activa la casilla Retrato de fases para mostrar el retrato de fases mejorado de $f(z)=1/z^2,$ con curvas de nivel del módulo.

Dominios simplemente y múltiples conexos

Decimos que un dominio $D$ es simplemente conexo si todo contorno cerrado simple $C$ que se encuentra completamente en $D$ puede contraerse a un punto sin salir de $D.$ Ver Figura 3. En otras palabras, si dibujamos cualquier contorno cerrado simple $C$ de modo que esté completamente contenido en un dominio simplemente conexo, entonces $C$ encierra únicamente puntos del dominio $D.$

Simply connected — Dominio simplemente conexo $D.$

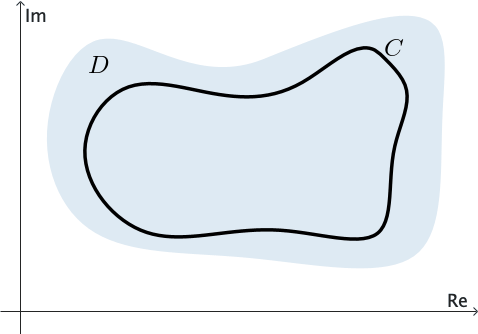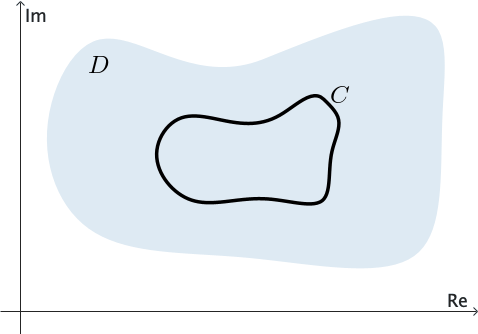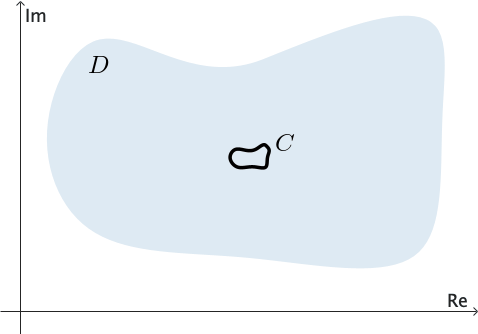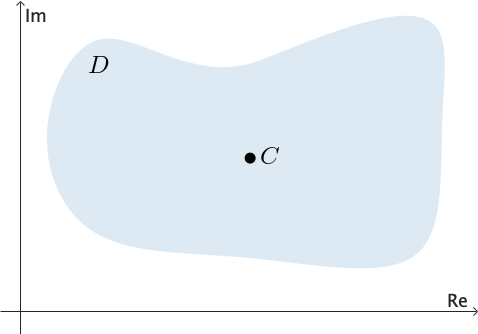
En otras palabras, un dominio simplemente conexo no tiene "agujeros". Todo el plano complejo es un ejemplo de un dominio simplemente conexo; el anillo definido por $1 \lt |z| \lt 2$ no es simplemente conexo.

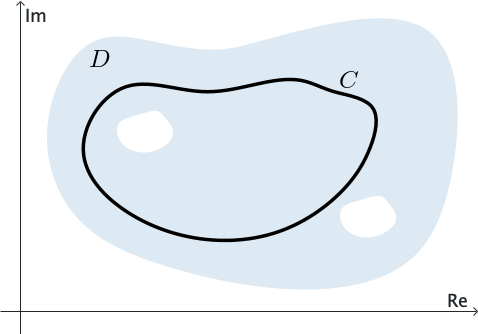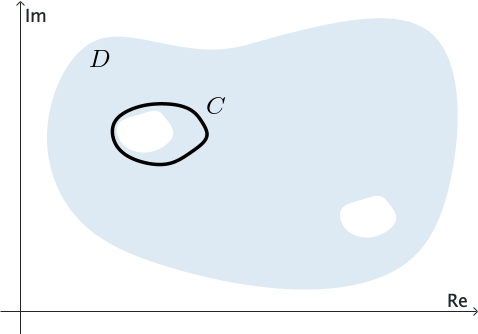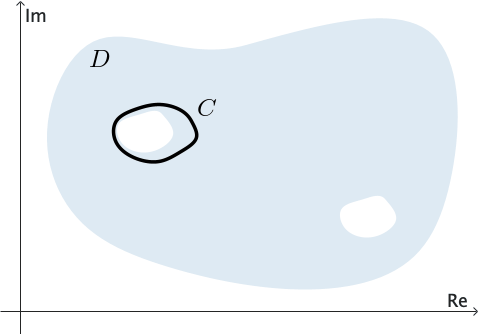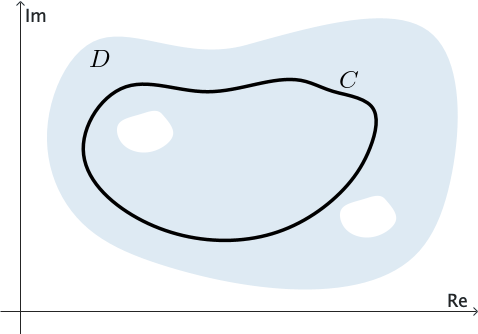
Un dominio que no es simplemente conexo se llama un dominio multiplemente conexo; es decir, un dominio multiplemente conexo tiene "agujeros". Por ejemplo, observa en la Figura 5 que si la curva $C$ que rodea el "agujero" (en el lado izquierdo) se reduce a un punto, la curva tendría que abandonar $D$ eventualmente.

No simply connected — Dominio no simplemente conexo $D$.

El contorno cerrado en el Teorema de Cauchy-Goursat no necesita ser simple cuando el teorema se adapta a dominios simplemente conexos. Es decir, el contorno puede cruzarse a sí mismo. El siguiente teorema permite esta posibilidad.

Si una función $f$ es analítica en todo un dominio simplemente conexo $D,$ entonces \[ \int_C f(z) \, dz = 0. \] para todo contorno cerrado $C$ contenido en $D.$

La demostración es sencilla si $C$ es un contorno cerrado simple o si es un contorno cerrado que se intersecta a sí mismo un número finito de veces. En el caso de que $C$ sea simple y esté contenido en $D,$ la función $f$ es analítica en cada punto interior y sobre $C.$ El Teorema de Cauchy-Goursat asegura que la conclusión del Teorema 3 se cumple. Por otro lado, si $C$ es cerrado pero se intersecta a sí mismo un número finito de veces, está compuesto por un número finito de contornos cerrados simples. Esto se ilustra en la Figura 6, donde los contornos cerrados simples $C_k$ $(k = 1, 2, 3, 4)$ forman $C.$ Como el valor de la integral alrededor de cada $C_k$ es cero, según el Teorema de Cauchy-Goursat, se deduce que

\begin{eqnarray*} \int_C f(z)\,dz = \sum_{k=1}^{4}\int_{C_k}f(z)\, dz = 0. \end{eqnarray*}

Simply closed contours C_k — Contornis simples cerrados $C_k.$

Ejemplo 4: Sea $C$ cualquier contorno cerrado contenido en el disco abierto $|z| \lt 2.$ Entonces \[ \int_C \frac{z\sin(z)}{\left(z^2-9\right)^3}dz =0. \] Nota que el disco es un dominio simplemente conexo y que las dos singularidades $z=\pm 3$ del integrando están fuera del disco.

Ejemplo del Teorema de Cauchy-Goursat — El disco abierto $D:|z|\lt 2$ es simplemente conexo y $C$ es cualquier contorno cerrado.

Una función $f$ que es analítica en todo un dominio simplemente conexo $D$ debe tener una antiderivada en todas partes dentro de $D.$

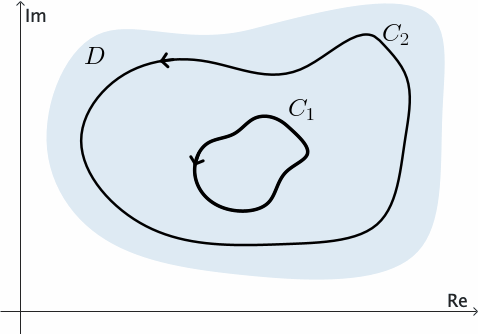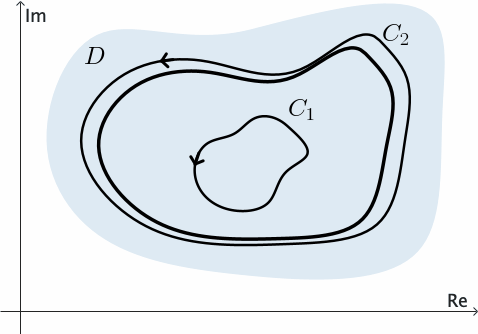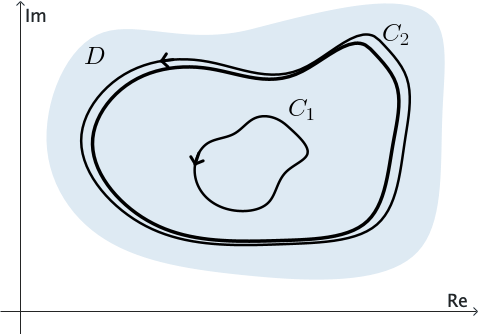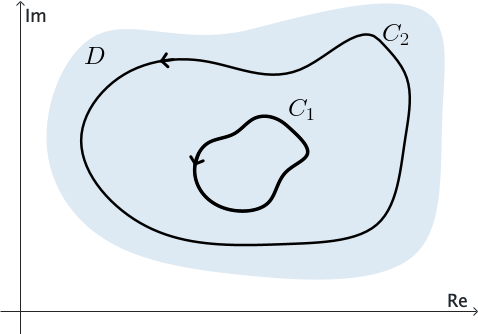
Si $f$ es analítica en un dominio múltiplemente conexo $D,$ entonces no podemos concluir que $\int_C f(z)\,dz=0$ para cada contorno cerrado simple $C$ en $D.$ Supongamos que $D$ es múltiplemente conexo con dos "agujeros". Sean $C,$ $C_1$ y $C_2$ contornos cerrados simples tales que cada $C_k$ rodea únicamente un "agujero" en el dominio y están contenidos dentro de $C.$ Véase la Figura 8.

Cauchy-Goursat Theorem multiply connected — $D$ es múltiplemente conexo con dos "agujeros".

Ahora, supongamos también que $f$ es analítica en cada contorno y a lo largo de todo el dominio múltiplemente conexo compuesto por los puntos dentro de $C$ y exteriores a cada $C_k.$ Supongamos que $C$ se describe en dirección antihoraria y cada $C_k$ se describe en dirección horaria. Introducimos un camino poligonal $L_1,$ que consiste en un número finito de segmentos de línea unidos extremo a extremo, para conectar el contorno exterior $C$ con el contorno interior $C_1.$ Como se muestra en la Figura 9, introducimos otro camino poligonal $L_2$ que conecta $C_1$ con $C_2;$ y finalmente otro camino poligonal $L_3$ que conecta $C_3$ con $C.$

Como se indica en la Figura 10, se pueden formar dos contornos cerrados simples $\Gamma_1$ y $\Gamma_2$, cada uno compuesto por caminos poligonales $L_k$ o $-L_k$ y partes de $C$ y $C_k$, y descritos en una dirección tal que los puntos encerrados por ellos queden a la izquierda. Aquí podemos aplicar el Teorema de Cauchy-Goursat a $f$ sobre $\Gamma_1$ y $\Gamma_2,$ y se encuentra que la suma de los valores de las integrales sobre esos contornos es cero. Como las integrales en direcciones opuestas a lo largo de cada camino $L_k$ se cancelan, sólo permanecen las integrales a lo largo de $C$ y de los $C_k$. Por lo tanto, obtenemos

\begin{eqnarray*} \int_C f(z)\,dz + \int_{C_1} f(z)\,dz + \int_{C_2} f(z)\,dz =0 \end{eqnarray*}

El siguiente teorema resume el resultado general para un dominio multiconectado con $n$ "agujeros."

Supongamos que:

$C$ es un contorno cerrado simple, descrito en la dirección antihoraria;
$C_k$ $(k = 1, 2, \ldots , n)$ son contornos cerrados simples interiores a $C$, todos descritos en la dirección horaria, que son disjuntos y cuyos interiores no tienen puntos en común.

Si $f$ es analítica en todos estos contornos y en todo el dominio multiconectado que consiste en los puntos dentro de $C$ y fuera de cada $C_k,$ entonces

\[ \int_C f(z)\,dz + \sum_{n=1}^{n} \int_{C_k} f(z)\,dz =0 \]

El siguiente corolario es conocido como el principio de deformación de contornos, ya que nos dice que si $C_1$ se deforma continuamente en $C_2$ pasando siempre por puntos en los cuales $f$ es analítica, entonces el valor de la integral de $f$ sobre $C_1$ nunca cambia.

Sea $C_1$ y $C_2$ contornos cerrados simples orientados positivamente, donde $C_1$ está en el interior de $C_2.$ Si $f$ es analítica en la región cerrada formada por dichos contornos y todos los puntos entre ellos, entonces \[ \int_{C_2} f(z) \, dz = \int_{C_1} f(z) \, dz . \]

Cauchy-Goursat Theorem — $C_1$ se deforma continuamente en $C_2$.

Ejemplo 5: Podemos usar el corolario anterior para demostrar que \[ \int_C \frac{1}{z} dz = 2\pi \,i \] para cualquier contorno cerrado simple orientado positivamente $C$ que rodee el origen.

Consideremos $C_0$, un círculo orientado positivamente con centro en el origen y radio lo suficientemente pequeño para que $C_0$ esté completamente dentro de $C.$

Sabemos que (ver ejemplo 2 en la sección de Integración Compleja) \[ \int_{C_0} \frac{1}{z} dz = 2\pi \,i. \] y dado que $1/z$ es analítica en todas partes excepto en $z = 0,$ el resultado se deduce fácilmente.

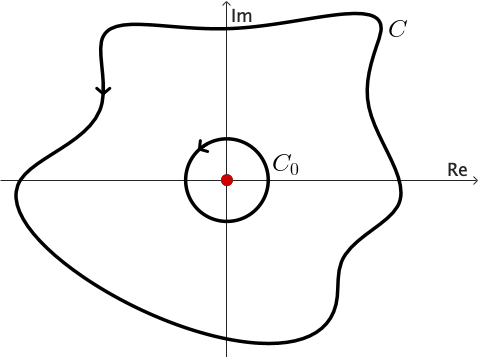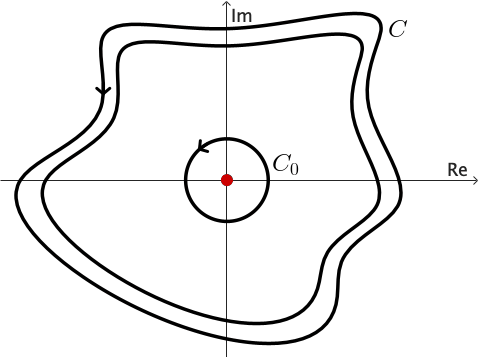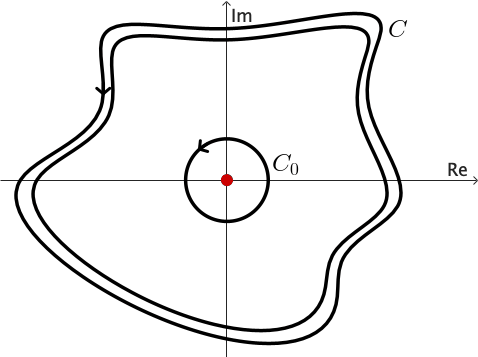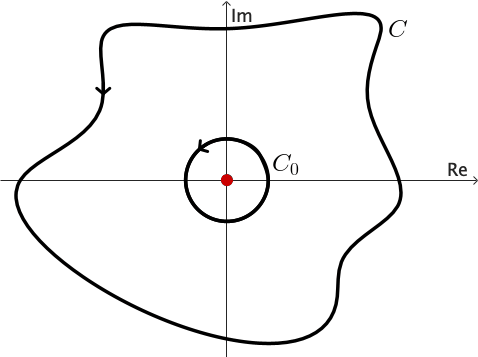
Ejercicio 1: Utiliza el principio de deformación de contornos para demostrar que si $z_0$ es una constante compleja interior a cualquier contorno cerrado simple $C,$ entonces para un número entero $n,$ se tiene \[ \int_C \frac{dz}{(z-z_0)^{n}} = \left\{ \begin{array}{ll} 2\pi i & n = 1,\\ 0, & n\neq 1. \end{array} \right. \]

Notas históricas y demostración

Cauchy comunicó por primera vez el teorema sobre la integral a la Académie des Sciences en 1814, como parte de un memorando relacionado con otros temas (integrales reales impropias) [1 pp. 132-133, 4, 13 pp. 56-57]. La primera forma general del teorema fue comunicada a la Académie en 1825 en un memorando titulado Mémoire sur les intégrales définies, prises entre des limites imaginaires [1 pp. 151-156, 5, 13 pp. 89-91].

Goursat presentó una demostración del Teorema de Cauchy en 1884 para el caso de una curva cerrada simple, dividiendo el interior en pequeños cuadrados, mostrando que la integral alrededor de cada cuadrado de lado $\ell$ está acotada por $\epsilon \ell ^2,$ y luego sumando los resultados. Para obtener esta estimación para cualquier $\epsilon$ necesita la continuidad uniforme de $f'$ [7]. En su artículo de 1900, Goursat finalmente eliminó la suposición de continuidad de $f'$ [2, 8]. El argumento es como antes, pero ahora subdivide cada cuadrado hasta que se cumple la estimación necesaria para cada uno de ellos, es decir,

\[ \left|f(z) - f(z_0) - f'(z_0)(z-z_0)\right|\lt \epsilon \left|z-z_0\right| \]

para cada $z$ en el borde del subcuadrado, donde $z_0$ es algún punto fijo en el subcuadrado. El punto importante aquí es que el mismo $\epsilon$ servirá para cada subcuadrado.

En 1900, Eliakim H. Moore refinó la demostración, abordando el tratamiento de la curva de contorno con mayor precisión [11]. También introdujo el enfoque moderno de la prueba por contradicción, que consiste en subdividir el dominio, seleccionar la región donde la conclusión se contradice de manera más significativa, y luego aplicar la definición de la derivada en el punto límite resultante [9, p. 651].

Más tarde, en 1901, Alfred Pringsheim presentó una crítica del tratamiento de Goursat sobre la curva de contorno [12]. Observó que estos problemas desaparecen cuando la técnica de la prueba se aplica a una forma geométrica básica, como un triángulo. Desde ahí, el teorema se extiende a caminos poligonales simples dentro de un dominio simplemente conexo mediante la triangulación del interior del camino. Finalmente, se puede generalizar a caminos arbitrarios aproximándolos con caminos poligonales. [9, p. 651]. Este es el método que utilizaremos para demostrar el Teorema de Cauchy-Goursat.

Para evitar repeticiones innecesarias a lo largo de la siguiente discusión, daremos por sentado que estamos trabajando en un dominio simplemente conexo $D$ y que $f$ representa una función compleja analítica en $D.$

Si $\Delta$ es un contorno triangular que yace completamente dentro de $D,$ entonces $\int_{\Delta} f(z)\,dz=0.$

Sea $\Delta$ el contorno triangular mostrado en la Figura 13. Los vértices de $\Delta$ están etiquetados como $V_1, V_2$ y $V_3.$ Formamos triángulos más pequeños $\Delta_1, \Delta_2, \Delta_3$ y $\Delta_4$ uniendo los puntos medios $M_1, M_2$ y $M_3$ de los lados de $\Delta$ mediante segmentos de línea recta, como se muestra en la Figura 14. Entonces

\begin{eqnarray}\label{sumcontours} \int_{\Delta} f(z)\,dz = \int_{C_1} f(z)\,dz +\int_{C_2} f(z)\,dz +\int_{C_3} f(z)\,dz +\int_{C_4} f(z)\,dz. \end{eqnarray}

Triangle in D. — Contorno triangular $\Delta$ en el interior de $D.$

Partition. — Contornos triangulares $C_k.$

Usando la desigualdad triangular, tenemos

\begin{eqnarray}\label{triangle01} \left|\int_{\Delta} f(z)\,dz\right| \leq \left|\int_{C_1} f(z)\,dz\right| + \left|\int_{C_2} f(z)\,dz\right| + \left|\int_{C_3} f(z)\,dz\right| + \left|\int_{C_4} f(z)\,dz\right|. \end{eqnarray}

Dado que las cuatro cantidades del lado derecho de la desigualdad anterior son números reales no negativos, y como consecuencia, una de ellas debe ser mayor o igual a las otras tres. Denotemos el contorno triangular de la integral con el mayor módulo por el símbolo $\Delta_1.$ Así \begin{eqnarray}\label{triangle02} \left|\int_{\Delta} f(z)\,dz\right| \leq 4 \left|\int_{\Delta_1} f(z)\,dz\right| . \end{eqnarray}

Ahora repetimos el proceso anterior para el triángulo $\Delta_1.$ Es decir, formamos triángulos dentro de $\Delta_1$ uniendo los puntos medios de sus lados mediante segmentos de línea de la misma manera que se muestra en la Figura 14 y procedemos con el equivalente de (\ref{sumcontours}) y (\ref{triangle01}). La integral de $f$ a lo largo de uno de estos nuevos contornos triangulares, llamémoslo $\Delta_2,$ entonces satisface \[ \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4 \left|\int_{\Delta_2} f(z)\,dz\right| . \]

Combinamos esta última desigualdad con (\ref{triangle02}) para obtener \[ \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4 \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4^2 \left|\int_{\Delta_2} f(z)\,dz\right| . \]

Continuamos de esta manera para obtener una secuencia de contornos triangulares "anidados" $\Delta, \Delta_1, \Delta_2, \ldots,$ es decir, cada triángulo en la secuencia está contenido en el inmediatamente anterior. Después de $n$ pasos obtenemos \begin{eqnarray}\label{bound4} \left|\int_{\Delta_1} f(z)\,dz\right| \leq 4^n \left|\int_{\Delta_n} f(z)\,dz\right| . \end{eqnarray}

Dado que la secuencia de contornos triangulares $\Delta, \Delta_1, \Delta_2, \ldots,$ está anidada, existe un punto $z_0$ en el dominio $D$ que es común a cada triángulo en la secuencia. Además, como $f$ es analítica, entonces $f'(z_0)$ existe. Si definimos \begin{eqnarray}\label{lambda} \Lambda(z) = \frac{f(z)-f(z_0)}{z-z_0} - f'(z_0), \end{eqnarray} entonces $\left|\Lambda(z)\right|$ puede hacerse arbitrariamente pequeño siempre que $z$ esté lo suficientemente cerca de $z_0$. Esto es cierto porque $f$ es analítica en $D$ y por lo tanto el límite \begin{eqnarray*} \lim_{z\to z_0}\frac{f(z)-f(z_0)}{z-z_0} \end{eqnarray*} existe y es igual a $f'(z_0).$ En otras palabras, para cada $\epsilon \gt 0,$ existe $\delta \gt 0$ tal que

\begin{eqnarray}\label{smallenough} \left|\Lambda(z)\right|\lt \epsilon \quad \text{siempre que}\quad \left|z-z_0\right|\lt \delta. \end{eqnarray}

Podemos resolver (\ref{lambda}) para $f(z)$ y reemplazar este valor en el integrando en (\ref{bound4}) para obtener

\begin{eqnarray}\label{expanded} \int_{\Delta_n}f(z)\,dz = f(z_0) \int_{\Delta_n}dz + f'(z_0)\int_{\Delta_n}(z-z_0)\,dz + \int_{\Delta_n}(z-z_0)\Lambda(z)\,dz. \end{eqnarray}

Dado que \[ \int_{\Delta_n}dz =0 \quad \text{y}\quad \int_{\Delta_n}(z-z_0)\,dz=0 \] (¿Por qué?), el lado derecho de (\ref{expanded}) se reduce a \begin{eqnarray}\label{reduced} \int_{\Delta_n}f(z)\,dz = \int_{\Delta_n}(z-z_0)\Lambda(z)\,dz. \end{eqnarray}

Ahora, sea $L$ y $L_1$ las longitudes de los contornos triangulares $\Delta$ y $\Delta_1,$ respectivamente. Luego, si tenemos en cuenta cómo se construyó el triángulo $\Delta_1$, es un problema sencillo en triángulos semejantes mostrar que $L_1$ está relacionado con $L$ por $L_1=\dfrac{1}{2}L.$ Del mismo modo, si $L_2$ es la longitud de $\Delta_2,$ entonces $L_2=\dfrac{1}{2}L_1 = \dfrac{1}{2^2}L.$ En general, tenemos que si $L_n$ es la longitud de $\Delta_n,$ entonces $L_n= \dfrac{1}{2^n}L.$

Para cualquier $z \in \Delta_n,$ tenemos que $\abs{z-z_0}\lt L_n,$ donde $\ds L_n= \frac{1}{2^n}L.$ Si elegimos $n$ lo suficientemente grande para que \[ \abs{z-z_0}\lt \frac{1}{2^n}L\lt \delta, \] se sigue de (\ref{reduced}), (\ref{smallenough}) y la desigualdad ML que

\begin{eqnarray}\label{boundgeneral} \abs{\int_{\Delta_n}f(z)\,dz } = \abs{ \int_{\Delta_n}(z-z_0)\Lambda(z)\,dz} \leq \frac{L}{2^n}\cdot \epsilon \cdot \frac{L}{2^n} = \frac{L^2}{4^n}\epsilon \end{eqnarray}

Al combinar (\ref{bound4}) con (\ref{boundgeneral}) obtenemos una cota para el módulo de la integral sobre $\Delta:$ \begin{eqnarray}\label{lastbound} \abs{\int_{\Delta}f(z)\,dz } \leq 4^n \frac{L^2}{4^n}\epsilon = L^2\epsilon. \end{eqnarray} Dado que $\epsilon \gt 0$ puede hacerse arbitrariamente pequeño, entonces $\abs{\int_{\Delta}f(z)\,dz}=0.$ Por lo tanto, \begin{eqnarray*} \int_{\Delta}f(z)\,dz =0. \end{eqnarray*}

If $C$ is a closed polygonal contour lying entirely within $D,$ then $\int_C f(z)\,dz=0.$

Ejercicio 2: Usa el Lema 1 y el hecho de que cualquier contorno poligonal cerrado $C$ puede ser "triangulado" para demostrar el Lema 2.

Triangulation of the polygonal contour — Triangulación del contorno poligonal $C.$

Observación: Aproximadamente, "triangulado" significa que el polígono cerrado $C$ puede descomponerse en un número finito de triángulos añadiendo líneas como se muestra en la Figura 16. Nota que luego podemos proceder como en la demostración de la Lemma 1 e integrar dos veces a lo largo de estos segmentos de línea añadidos, pero en direcciones opuestas. Si el polígono cerrado $C$ tiene $n$ lados, entonces puede descomponerse en $n$ triángulos $C_1, C_2, \ldots, C_n$ y eventualmente llegaremos a la siguiente análoga de (\ref{sumcontours}): \[ \int_C f(z)\,dz = \sum_{k=1}^{n} \int_{C_k}f(z)\,dz. \]

Ahora, el Teorema de Cauchy-Goursat puede demostrarse fácilmente usando la Lemma 2 y el hecho de que cualquier contorno cerrado $C$ puede ser aproximado con el grado de precisión deseado por una trayectoria cerrada poligonal.

Approximation by polygonal path — El contorno $C$ es aproximado por un contorno poligonal $P.$

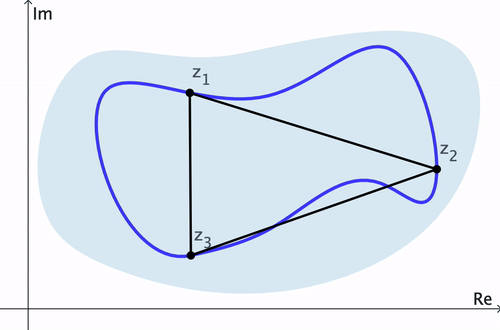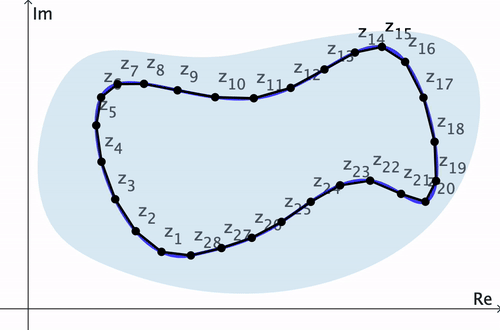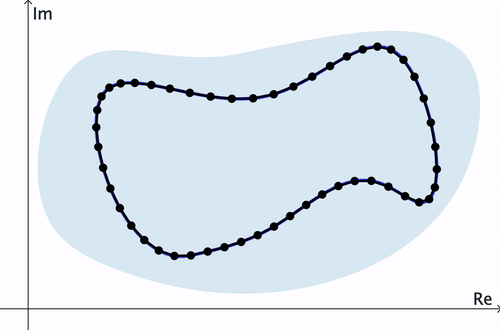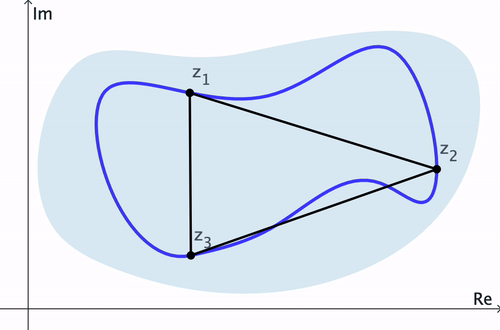
Demostración del Teorema de Cauchy-Goursat. Consideremos un contorno cerrado simple $C$ y $n$ puntos $z_1, z_2, \ldots, z_n$ en $C$ a través de los cuales se ha construido un camino poligonal $P$. Entonces se puede demostrar que la diferencia \[ \abs{\int_C f(z)\,dz - \int_P f(z)\,dz} \] puede hacerse arbitrariamente pequeña cuando $n \to \infty.$ Así, por el Lema 2, $\ds \int_P f(z)\,dz = 0$ para cualquier $n.$ Por lo tanto, $\ds \int_C f(z)\,dz=0.$ $\hspace{10pt}\blacksquare$

El Teorema de Cauchy-Goursat ha sido establecido a través de varios métodos. Por ejemplo, se han construido demostraciones específicamente para rectángulos o discos (ver [3, 10]). Más allá de estos enfoques, se han desarrollado muchas otras demostraciones del teorema. Cabe destacar que John D. Dixon presentó una demostración concisa y elegante que depende únicamente de los conceptos fundamentales de la teoría de funciones complejas en conjuntos convexos [6]. Por otro lado, Rudolf Výborný ofreció una demostración basada en homotopía diferenciable [14].

Referencias

Bottazzini, U. (1984). The higher calculus: a history of real and complex analysis from Euler to Weierstrass. New York : Springer-Verlag.
Borger, R. L. (1921). On the Cauchy-Goursat theorem, Bulletin of the American Mathematical Society, Vol. 27, No. 7, pp. 325-329.
Brown, J. W., Churchill, R. V. (2009). Complex Variables and Applications. 8th Edition. New York: McGraw-Hill Higher Education.
Cauchy, A. (1814). Mémoire sur la théorie des intégrales définies, in Œuvres complètes d'Augustin Cauchy, $\text{I}^{re}$ série, vol. I, Gauthier Villars, Paris.
Cauchy, A. (1825). Mémoire sur les intégrales définies, prises entre des limites imaginaires, in Œuvres complètes d'Augustin Cauchy, $\text{II}^{e}$ série, vol. XV, Gauthier Villars, Paris.
Dixon, J. D. (1971). A brief proof of Cauchy's integral theorem, Proceedings of the American Mathematical Society, Vol. 29, No. 3, pp. 625-626.
Goursat, E. (1884). Démonstration du théorème de Cauchy. Acta Mathematica, 4, pp. 197-200.
Goursat, E. (1900). Sur la définition générale des fonctions analytiques, d'après Cauchy, Transactions of the American Mathematical Society, Vol. 1, No. 1, pp. 14-16.
Hance-Olsen, H. (2008). On Goursat's Proof of Cauchy's Integral Theorem, The American Mathematical Monthly, 115, pp. 648-652.
Marsden, J. E. & Hoffman, M. J. (1999) Basic Complex Analysis. (3rd ed.) New York: W. H. Freeman and Co.
Moore, E. H. (1900). A Simple Proof of the Fundamental Cauchy-Goursat Theorem, Transactions of the American Mathematical Society, Vol. 1, No. 4, pp. 499-506.
Pringsheim, A. (1901). Ueber den Goursat'schen Beweis des Cauchy'schen Integralsatzes, Transactions of the American Mathematical Society, Vol. 2, No. 4, pp. 413-421.
Smithies, F. (1997). Cauchy and the Creation of Complex Function Theory. UK: Cambridge University Press.
Výborný, R. (1979). On the Use of a Differentiable Homotopy in the Proof of the Cauchy Theorem, The American Mathematical Monthly, Vol. 86, No. 5, pp. 380-382.