Cargando...
Fórmula Integral de Cauchy Tabla de Contenidos Análisis Complejo Series


El Teorema Fundamental
del Álgebra

Consideremos el polynomio

\begin{eqnarray}\label{example-001} p(z) = z^8-2z^7+2z^6-4z^5+2z^4-2z^3-5z^2+4z-4 \end{eqnarray}

El Teorema Fundamental del Álgebra establece que: Cada polinomio no constante con coeficientes complejos tiene una raíz en los números complejos.

Polynomial of degree 8
Retrato de fase mejorado de $p(z),$ con curvas de nivel de $\abs{p(z)}.$

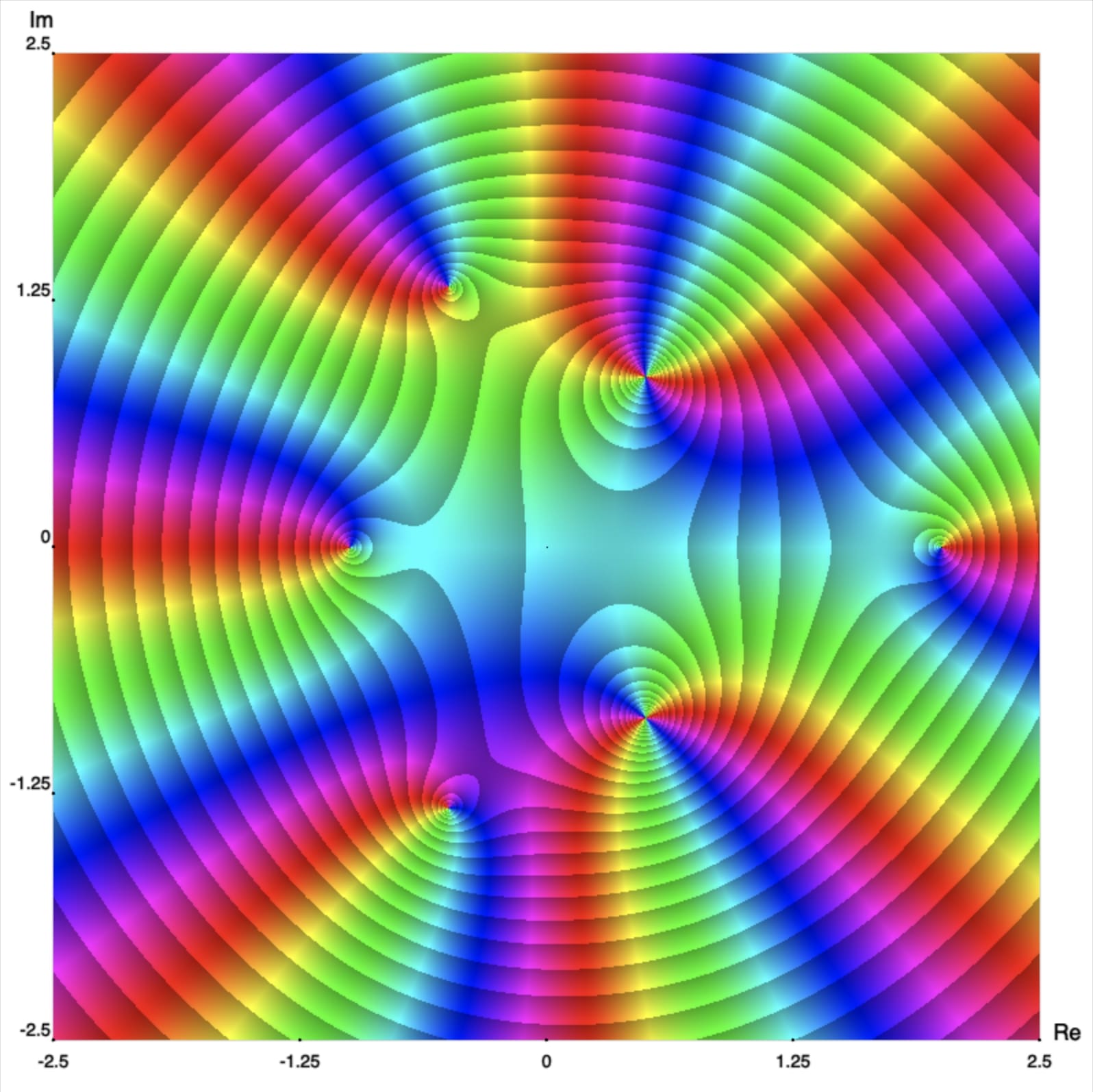
La Figura 1 muestra un retrato de fase mejorado, con curvas de nivel del módulo, del polinomio definido en (\ref{example-001}). Lo primero que se nota en esta imagen es que, efectivamente, el Teorema Fundamental del Álgebra se cumple para $p(z).$ Recuerda que podemos identificar fácilmente las raíces, o ceros, de funciones complejas utilizando retratos de fase mejorados. Solo necesitamos buscar los puntos donde todos los colores se encuentran. En la Figura 1, podemos ver claramente que hay seis puntos donde todos los colores se encuentran, lo que significa que $p(z)$ tiene 6 raíces. ¿Por qué $p(z),$ un polinomio de grado ocho, tiene solo seis raíces? La razón es que dos de las raíces son raíces dobles (también decimos que su multiplicidad es dos), y este hecho también es evidente en la imagen. Las raíces simples se encuentran en \[ -1, \;\; 2, \;\; \frac{-1\pm i \sqrt{7}}{2}, \] y las raíces dobles están en \[ \frac{1\pm i \sqrt{3}}{2}. \] El siguiente applet muestra todas las raíces. Además, puedes apreciar su multiplicidad, la cual está indicada por el número de veces que los colores se repiten. Por ejemplo, en las raíces dobles, los colores del matiz se repiten dos veces, mientras que en las raíces simples se repiten solo una vez. Activa las casillas para resaltar las raíces.


Otra propiedad fascinante del polinomio $p(z)$ se puede visualizar de la siguiente manera. Considera un círculo centrado en el origen con radio $r,$ elegido de manera que todas las raíces de $p(z)$ se encuentren dentro de este círculo. Cuando este círculo es transformado por $p(z),$ su imagen se convierte en una curva cerrada que se envuelve alrededor del origen exactamente ocho veces. Este comportamiento se ilustra en el applet a continuación. A la izquierda, se muestran las raíces de $p(z)$ y el círculo. A la derecha, puedes ver la correspondiente imagen del círculo, mostrando claramente el efecto de envolvimiento. Simplemente arrastra el control deslizante de abajo.


Demostración y notas históricas

La desigualdad de Cauchy se puede usar para demostrar el siguiente resultado, nombrado en honor al matemático Francés Joseph Liouville:

(Teorem de Liouville) Las únicas funciones enteras acotadas son constantes.
Supongamos que $f$ es entera y acotada, es decir, $\abs{f(z)}\lt M$ para todo $z.$ Entonces, para cualquier punto $z_0,$ la desigualdad de Cauchy nos da \[ \abs{f'(z)}\leq \frac{M_r}{r}. \] Al hacer $r$ arbitrariamente grande, podemos hacer $\abs{f'(z)}$ tan pequeño como queramos. Esto significa que $f'(z_0)= 0$ para todos los puntos $z_0$ en el plano complejo. Por lo tanto, según el Teorema 3 en la sección de Diferenciación Compleja, $f$ debe ser constante.

Ahora con el Teorema de Liouville podemos demostrar fácilmente:

(Teorema Fundamental del Álgebra) Todo polinomio \[ p(z)= a_n z^n+ a_{n-1}z^{n-1}+\cdots + a_1z+ a_0\quad (a_n\neq 0) \] de grado $n\geq 1$ tiene al menos un cero.
Demostraremos esta afirmación por contradicción. Supongamos que $p(z)$ no es cero para ningún valor de $z,$ entonces \[ f(z) = \frac{1}{p(z)} \] es una función entera. Dado que $\abs{p(z)}\to \infty$ cuando $\abs{z}\to \infty,$ existen $M$ y $R\gt 0$ tales que $\abs{p(z)}\gt M$ si $\abs{z}\gt R.$ Esto implica que para $\abs{z}\gt R,$ \[ \abs{f(z)} = \abs{\frac{1}{p(z)}} \lt \frac{1}{M}. \] Ahora, $f$ es continua en la región $\abs{z}\leq R,$ la cual es cerrada y acotada. Según el Teorema 3, en la sección de Continuidad, $f$ también está acotada para $\abs{z}\leq R.$ Por lo tanto, $f(z)$ está acotada en todo el plano complejo. El Teorema de Liouville implica entonces que $f(z)$ es constante, y, en consecuencia, $p(z)$ también es constante. Pero esto es una contradicción. Concluimos que debe existir al menos un número $z$ para el cual $p(z) = 0.$

Se deduce de la manera habitual que cualquier polinomio $p(z)$ de grado $n,$ con coeficientes complejos, puede expresarse como un producto de términos lineales: \begin{eqnarray}\label{factorized} p(z) = c\left(z-\alpha_1\right)\left(z-\alpha_2\right)\cdots \left(z-\alpha_n\right), \end{eqnarray} donde $c$ y $\alpha_k$ $(k=1,2,\ldots, n)$ son constantes complejas. Por supuesto, algunas de las constantes $\alpha_k$ en la expresión (\ref{factorized}) pueden aparecer más de una vez, y es claro que $p(z)$ no puede tener más de $n$ ceros distintos.

Según B. Fine & G. Rosenberger [7, Capítulo 1], el Teorema Fundamental del Álgebra fue mencionado por primera vez por Peter Roth de Núremberg en 1608. Sin embargo, también se le atribuye a Albert Girard, quien enunció el resultado en 1629. Más tarde, René Descartes proporcionó una formulación más clara en 1637, distinguiendo entre raíces reales e imaginarias. La primera demostración publicada del teorema fue presentada por Jean le Rond d'Alembert en 1746, aunque contenía lagunas significativas. La primera demostración ampliamente aceptada fue presentada por Carl Friedrich Gauss en su tesis doctoral de 1797, publicada en 1799 [8]. Curiosamente, los investigadores modernos señalan que la demostración original de Gauss tiene tantas lagunas como la de d'Alembert (ver, por ejemplo, [12, 14]). No obstante, Gauss produjo tres demostraciones más rigurosas: dos publicadas en 1816 y una versión final, esencialmente una refinación de su primera demostración, presentada en 1849 [9].

Esquema de la demostración original de Gauss: Dado que $p(z)$ es un número complejo para cualquier $z\in \C$ y dado que $z=x+iy$ con $x,y\in \R,$ tenemos que \[ p(z) = u(x,y) + i v(x,y). \] Las ecuaciones $u(x,y)=0$ y $v(x,y)=0$ representan entonces curvas en el plano $\R^2.$ Mediante un análisis cuidadoso de las posibles funciones $u(x,y),$ $v(x,y)$ para un polinomio complejo $p(z),$ Gauss demostró que las curvas $u(x,y)=0$ y $v(x,y)=0$ deben tener una solución común $(x_0, y_0).$ El número complejo $z_0= x_0+iy_0$ es entonces la raíz de $p(z).$

Por ejemplo, la Figura 2 muestra las curvas $u(x,y)=0$ y $v(x,y)=0$ para nuestro polinomio inicial $p(z) = z^8-2z^7+2z^6-4z^5+2z^4-2z^3-5z^2+4z-4.$

Real and imaginary components of a polynomial
Las curvas $u(x,y)=0$ (Rojo) y $v(x,y)=0$ (Azul) de $p(z).$ Las raíces están representadas por los puntos $Z_k$.

Aunque se argumenta que las primeras demostraciones de Gauss del Teorema Fundamental del Álgebra también incluían algunas lagunas, aún muestran de manera intuitiva por qué cualquier polinomio complejo debe tener una raíz. Hoy en día, existen muchas demostraciones conocidas de este teorema, incluidas demostraciones que utilizan métodos de álgebra abstracta, análisis y topología. Las referencias incluyen muchos artículos y libros con demostraciones de este teorema; por ejemplo, [7] por sí solo contiene 11 demostraciones.


Referencias

  1. Abian, A. (1986). A new proof of the fundamental theorem of algebra, Caribbean J. Math. 5, no. 1, 9-12.
  2. Bennish, J. (1992). Another proof of the fundamental theorem of algebra, Amer. Math. Monthly, 99, 426.
  3. Boas, Jr., R. P. (1935). A proof of the fundamental theorem of algebra, Amer. Math. Monthly, 42, 501-502.
  4. Boas, Jr., R. P. (1964). Yet another proof of the fundamental theorem of algebra, Amer. Math. Monthly, 71, 180.
  5. Byl, J. (1999). A simple proof of the fundamental theorem of algebra, Internat. J. Math. Ed. Sci. Tech. 30, no. 4, 602-603.
  6. Fefferman, C. (1967). An easy proof of the fundamental theorem of algebra, Amer. Math. Monthly, 74, 854-855.
  7. Fine, B. & Rosenberger. G. (1997). The Fundamental Theorem of Algebra. New York: Springer-Verlag Inc.
  8. Gauss, C. F. (1799). Demonstratio nova theorematis omnem functionem algebraicum rationalem integram unius variabilis in factores reales primi vel secundi gradus resolvi posse, Helmstedt dissertation, reprinted in Werke, Vol. 3, 1-30.
  9. Gauss, C. F. (1850). Beiträge zur Theorie der algebraischen Gleichungen". Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 4: 34-35.
  10. Redheffer, R. M. (1964). What! Another note just on the fundamental theorem of algebra? Amer. Math. Monthly, 71, 180-185.
  11. Sen, A. (2000). Fundamental theorem of algebra—yet another proof, Amer. Math. Monthly, 107, 842-843.
  12. Stillwell, J. (1989). Mathematics and its History. New York: Springer-Verlag.
  13. Velleman, D. J. (1997). Another proof of the fundamental theorem of algebra, Math. Mag. 70(1997), 216-217.
  14. Vellemen, D. J. (2015). The Fundamental Theorem of Algebra: A Visual Approach, The Mathematical Intelligencer, Vol. 37, pp. 12-21.

Series